Due to the capability of carrying orbital angular momentum (OAM) and possessing distinctive polarization characteristics, vector vortex beams (VVBs) are widely applied in the fields of super-resolution microscopy^[1,2], molecule orientation imaging^[3], and mode-division multiplexing (MDM)^[4–6]. In particular, focusing radially polarized light can create a strong longitudinally electrical component at the focus, while tightly focused azimuthally polarization leads to a strong axial magnetic field and a vanishing electric field^[2,3]. Among them, cylindrical vector beams, as orthogonal eigenmodes, offer more available high-order modes, which can further expand the communication capacity in multi-mode fibers. Through vector-eigenmodes (VMs) modulation, linearly polarized (LP) or circularly polarized (CP) OAM can be exploited as information channels^[7]. However, due to mode coupling and interference in fibers, hybrid VMs are inevitably involved in the transmission. Therefore, there is a challenge in identifying modal coefficients in the fields of optical communication and fiber MDM.

In recent years, modal decomposition (MD) techniques based on numerical methods, such as inverse matrix decomposition^[8,9] and the stochastic parallel gradient descent (SPGD) algorithm^[10,11], have rapidly become essential tools for revealing the characteristics of optical field modes. However, they may suffer from the drawback of falling into local optimal solutions. Meanwhile, deep learning (DL) algorithms, especially convolutional neural networks (CNN), have shown promise in the field of optics due to their powerful global search capabilities^[12–14], but most of them are retrieved based on only-intensity beam distributions. More polarization-projected intensity distributions azimuthally across the transversal beam are necessary to differentiate high-order degenerate VMs, which will lead to training computational costs for the DL process increasing greatly. The common concern is that DL-based networks are typically trained on simulated data and then applied to experimental data. Due to the lack of an equivalent relationship between simulated and experimental data, the reliability of experimentally reconstructed modal results cannot be guaranteed.

Here, to address these issues, we first attempt to validate the modal coefficients of the measured hybrid VVBs using the DL-based SPGD algorithm by retrieving multiplex polarized intensities, instead of only considering the beam intensity. Leveraging the correspondence between the waveplate angles and the modal coefficients, as well as polarization characteristics of the hybrid VMs, Xception models with different channel numbers are trained based on the simulation data and selected to decompose the intensity distribution of four polarization directions. In combination with the SPDG algorithm, Xception-based predictions of modal coefficients and modal intensity reconstruction in VM and OAM bases are obtained. This method successfully makes an accurate prediction of modal coefficients, which is validated through theoretical calculations based on the waveplate angles, demonstrating a high correlation of up to 99.65%. Second, modal coefficients of typically mixed VVBs are qualitatively analyzed in the form of VM and OAM mode bases. Finally, modal coefficients of first-order and second-order degenerate eigenmodes in few-mode fibers (FMF) by all-fiber mode-selective couplers (MSCs) are reconstructed. The universality of the DL-SPGD algorithm is demonstrated through the precise reconstruction of high-order VMs, which greatly promotes the accurate characteristics of VVBs in laser beam characterization, MDM, and other optical communication fields.

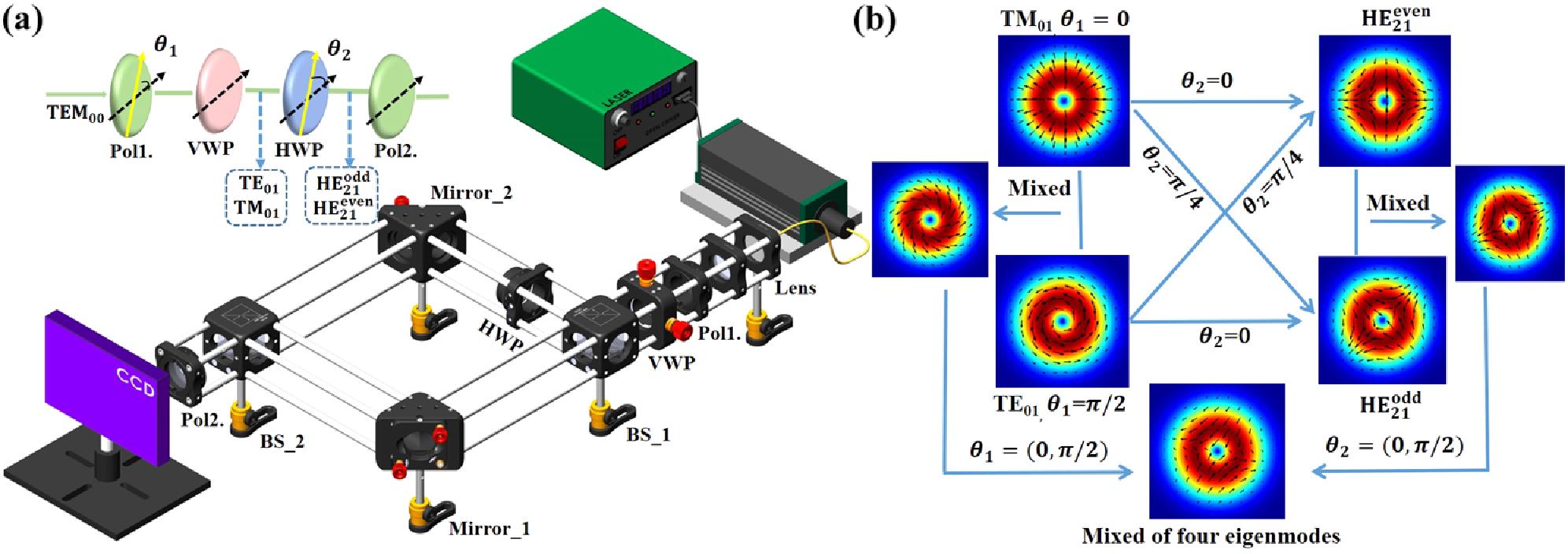
The first-order VM division multiplexing setup based on a vortex waveplate (VWP) is constructed based on the configuration of a Mach–Zehnder interferometer, as shown in Fig. 1(a). The fundamental mode Gaussian beam (${\mathrm{TEM}}_{00}$) emitted by a laser source ($\lambda =532\mathrm{nm}$) is collimated by a lens and converted into a uniformly LP beam by a polarizer (Pol1). ${\mathrm{TE}}_{01}$, ${\mathrm{TM}}_{01}$, or their admixture can be generated with appropriate polarized light passing through the VWP. Then, through a non-polarization beam splitter (BS), one way transmits ${\mathrm{TM}}_{01}$ and ${\mathrm{TE}}_{01}$ modes, and those of another way are transformed into ${\mathrm{HE}}_{21}^{\mathrm{even}}$ or ${\mathrm{HE}}_{21}^{\mathrm{odd}}$ modes after passing a half-wave plate (HWP)^[15,16]. A charge-coupled device (CCD) is used to record modal polarized field distribution of the VMs after passing another polarizer (Pol2). The multiplexing VM field distributions can be expressed as $$E_{\text{in}}=\sum _{k=1}^4{\rho }_k{e}^{i{\theta }_k}{E}_k,$$(1)where ${\rho }_k$, ${\theta }_k$, and $E_k$ correspond to the field amplitude, phase, and electric field of the VMs, respectively.

The transformation relationship between the VMs by changing the waveplate angles is shown in Fig. 1(b). Relative to the fixed VWP, ${\theta }_1$ and ${\theta }_2$ are defined as the angles of Pol1 and the HWP, which can be precisely rotated to convert the VMs through phase geometry transformation of the VWP. By adjusting different angles of ${\theta }_1$ and ${\theta }_2$, the mixed VMs with different weights among them can be obtained. It is noteworthy that the waveplates introduce an inherent phase difference of $\pm \pi /2$ between TM₀₁/TE₀₁ and ${\mathrm{HE}}_{21}^{\mathrm{even}}/{\mathrm{HE}}_{21}^{\mathrm{odd}}$. Additionally, a 50:50 BS divides the input light into two parts, which means $${\rho }_{{\mathrm{TM}}_{01}}+{\rho }_{{\mathrm{TE}}_{01}}={\rho }_{{\mathrm{HE}}_{21}^{\mathrm{eve}n}}+{\rho }_{{\mathrm{HE}}_{21}^{\mathrm{odd}}}=0.5,$$(2)where ${\rho }_{{\mathrm{TM}}_{01}}$, ${\rho }_{{\mathrm{TE}}_{01}}$, ${\rho }_{{\mathrm{HE}}_{21}^{\mathrm{eve}n}}$, and ${\rho }_{{\mathrm{HE}}_{21}^{\mathrm{odd}}}$ correspond to the weight coefficients of VMs.

In this Letter, Xception is chosen as the CNN model because of its unique network structure. It has depthwise separable convolutions, which can significantly reduce the number of parameters and improve the training efficiency^[17]. Because the VMs have non-uniform spatial polarization characteristics, the training images with the resolution of $128\times 128$ used in this model are taken from their polarization projected intensity patterns. For the first- and second-order VMs, four intensity patterns of polarization direction at 0°, 45°, 90°, and 135° are sufficient to reveal the polarization properties of the VMs. As shown in Fig. 2, two schemes of pattern-structured data are compared during the Xception-based DL process. One is the $N$-channel (here, $N$ is 4) image data, and the other is the $2\times 2$ matrix image data formatted with the resolution of $256\times 256$ as a multi-view image. Furthermore, more polarized intensities at a smaller angle separation are desirable for higher-order VMs, but it will result in more channel numbers for the training scheme or increase the resolution of multi-view images for the training process.

The entire flow of the DL-SPGD algorithm is shown in Fig. 2. The dataset of 40,000 random patterns is first trained in the Xception model for testing prediction. Then, the rough modal coefficients ${\rho }_o$ and ${\phi }_o$ are used as the initial values of the SPGD algorithm for accurate modal reconstruction. After certain iterations, predicted modal coefficients in the VM bases and reconstructed modal patterns using the DL-SPGD are obtained, which can be further converted to LP-OAM or CP-OAM bases using the matrix transformation of degenerating mode bases^[7].

First, the performance comparison of different channel numbers is presented in Table 1. Validation loss is a crucial metric for evaluating the performance of network models, which are calculated here using the mean squared error between the output and label vectors. $$V=\sum _{i=1}^M\sum _{j=1}^{2L-1}\frac{{(y_o^i[j]-y_l^i[j])}^2}{M},$$(3)where $y_o$ and $y_l$ represent the output and label vectors, respectively. The vector length ($2L-1$) of both first- and second-order VMs is seven, including four weight coefficients and three relative phase differences. $M$ represents the training batch size to be 10. To evaluate the predictive performance, the average error of modal coefficients is calculated, which comprises the modal weight errors $\mathrm{\Delta }\rho =|{\rho }_o^2-{\rho }_l^2|$ and relative phase error $\mathrm{\Delta }\theta =||{\theta }_o|-|{\theta }_l||/2\pi$. Additionally, model correlation is another metric used to demonstrate the accurate precision of predicted modal coefficients. Here, the correlation is denoted as $$J=\left|\frac{\iint [I_{\text{re}}(r,\phi )-\overline{I_{\text{re}}(r,\phi )}][I_{\mathrm{pre}}(r,\phi )-\overline{I_{\mathrm{pre}}(r,\phi )}]r\mathrm{d}r\mathrm{d}\phi }{\sqrt{\iint {[I_{\text{re}}(r,\phi )-\overline{I_{\text{re}}(r,\phi )}]}^{2}r\mathrm{d}r\mathrm{d}\phi \iint {[I_{\mathrm{pre}}(r,\phi )-\overline{I_{\mathrm{pre}}(r,\phi )}]}^{2}r\mathrm{d}r\mathrm{d}\phi }}\right|,$$(4)where $\overline{I_{\text{re}(\mathrm{pre})}(r,\phi )}$ represents the reconstructed or predefined mean intensity. Compared to the 4-channel model, the 1-channel model can reduce the number of convolution operations, resulting in a shorter training duration. From Table 1, it also can be seen that the performance of the 1-channel data can excel over that of the 4-channel data because less information is lost in the training process and polarization-dependent intensity information is embedded in the matrix patterns.

Based on the performance evaluation and polarization characteristics of the VMs, the validation loss curves are seen in Fig. 3(a), which show a fast convergence after about 90 epochs and a similar loss trend for the first- and second-order VMs. The results indicate that the feature of the matrix pattern can be learned well with a low loss. Another dataset with 1000 polarized intensity pattern is tested, and the average modal error of weights and phases is lower than 0.89% and 0.76%, as shown in Fig. 3(b). It is worth noting that the modal coefficient errors of low-order VMs are smaller than those of high-order ones. This might be understood because high-order VMs possess complicated intensity and polarization distribution.

Second, compared to that from the SPGD algorithm with inputting random coefficients, the predicted modal ones from the Xception-based DL process can not only efficiently acquire convergence with fewer iterations but also improve the accuracy of correction, as shown in Fig. 3(c). The comparisons between given and predicted modal coefficients using DL-SPGD algorithms for first-order VMs are shown in Fig. 3(d). It can be seen that the modal coefficients reconstructed by the DL-SPGD algorithm are closer to the given ones, and the correlation reaches 99.997%. This is due to the fact that the DL-SPGD algorithm perfectly combines the global optimization of DL and the accurate research capability of the SPGD.

Third, we attempt to experimentally validate the modal coefficients of measured VMs through DL-based SPGD algorithm. The modal weights can be calculated based on the Jones Matrix transformation of waveplates at different angles (${\theta }_1$ and ${\theta }_2$). The modal pattern generated as ${\theta }_1=\pi /8$ and ${\theta }_2=\pi /16$ is reconstructed in Fig. 4(a), and the reconstructed polarization beam profiles have great consistency with the measured ones. Accurate predictions of modal coefficients of the experimental pattern in the VMs base are achieved, as shown in Fig. 4(b), with a correlation of 99.57%. Moreover, according to the transformation between VM and LP-OAM and CP-OAM bases, their measured and predicted modal weights and relative phases are compared in Figs. 4(c) and 4(d). It should be noted that there are opposite modal phases with the same modal weights because of the phase ambiguity. Modal coefficients cannot be determined solely based on the four polarization projected intensity patterns. By utilizing pattern interference, the phase distribution can be examined, thereby obtaining unique predicted mode coefficients that correspond to the theoretical values.

Fourth, the predicted and measured modal coefficients are consistent at any admixture of VMs, which further validates the efficient decomposition using the DL-SPGD algorithm. As shown in Fig. 5, the mixed ${\mathrm{TM}}_{01}$ and ${\mathrm{TE}}_{01}$ or the mixed ${\mathrm{HE}}_{21}$ with variable modal weights in two paths of the Mach–Zehnder interferometer are combined to constitute the hybrid VMs, which are determined by the orientation of the VWP and HWP. The modal weights of ${\mathrm{TE}}_{01}$ and ${\mathrm{TM}}_{01}$ are determined by the input polarization direction relative to the VWP $({\theta }_1)$. When ${\theta }_1$ is fixed, the mode coefficients of TE₀₁ and TM₀₁ remain constant, while, by rotating ${\theta }_2$, the modal weights of ${\mathrm{HE}}_{21}^{\mathrm{even}}$ and ${\mathrm{HE}}_{21}^{\mathrm{odd}}$ modes show periodic changes. The dependences of their modal weights on the angles are shown in Figs. 5(a)–5(d), which demonstrate excellent agreement between measured and predicted modal weights, and an average correlation reaches up to 99.65%. This proves that the DL-SPGD algorithm can effectively provide accurate predictions for experimental data.

Two typical mixed VMs by mode superposition are marked as points A and B in Figs. 5(c) and 5(d), which are considered as degenerate odd and even modes of the same order VMs with a phase difference of $\pi /2$. Through matrix transformation of degenerating mode bases, the hybrid VM (point A) is described as ${\mathrm{TM}}_{01}+i{\mathrm{HE}}_{21}^{\mathrm{odd}}=\overline{x}{OAM}_{-1}+i\overline{y}{OAM}_{+1}$, and another hybrid VM (point B) is seen as ${\mathrm{TM}}_{01}-i{\mathrm{HE}}_{21}^{\mathrm{even}}+i{\mathrm{HE}}_{21}^{\mathrm{odd}}-{\mathrm{TE}}_{01}=\overline{x}{OAM}_{-1}-\overline{y}{OAM}_{+1}$. These mixed OAM modes can be separated using a polarizer, and their interference patterns are observed, as shown in Figs. 5(e2), 5(f2) and 5(e3), 5(f3), respectively. It is seen that there is only $\overline{x}OA{M}_{-1}$ at 0° polarization and only $\overline{y}OA{M}_{+1}$ at 90° polarization. Therefore, rotating the direction of the polarizer, the output modes can be switched between positive and negative topological charges of OAM.

Finally, through the precise reconstruction of high-order VM generation using all-fiber MSCs, we demonstrate high-order VM decomposition based on the DL-SPGD algorithm. The measured and predicted patterns of the first- and second-order hybrid VMs are shown in Figs. 6(a1) and 6(b1), respectively. It is found that their measured beam profiles have great consistency with the reconstructed ones. Among them, their intensity distributions with spatially LP-mode separations are non-uniform and polarization-dependent, which can be reconstructed more accurately using multi-view images. The predicted modal coefficients of the first-order VMs are shown in Fig. 6(a2), in which ${\mathrm{HE}}_{21}^{\mathrm{odd}}$ is dominated for a larger proportion of over 77% and has a phase difference of 1.726 with ${\mathrm{TM}}_{01}$. As shown in Fig. 6(b2), the second-order VMs with the prediction coefficients of ${\mathrm{HE}}_{31}^{\mathrm{odd}}$ and ${\mathrm{EH}}_{11}^{\mathrm{even}/\mathrm{odd}}$ are more than 99%, and there is a phase difference close to $\pi /2$ between ${\mathrm{HE}}_{31}^{\mathrm{even}/\mathrm{odd}}$ and ${\mathrm{EH}}_{11}^{\mathrm{even}}$. Their predicted modal coefficients in the OAM base are shown in Figs. 6(a3), 6(a4), 6(b3), and 6(b4). The predicted patterns expressed in the VM and OAM bases are self-consistent with the measured patterns. In a word, our proposed algorithm for high-order VM decomposition maintains high accuracy in the practical experiment. Of course, it is desirable to use more polarization intensities as multi-view images to reveal the polarization characteristics, but this would increase the calculation amount and reduce the calculation efficiency for multi-channel data.

In summary, the applicability of the DL-SPGD algorithm to high-order vector-eigenmode decomposition is verified based on multiple polarized intensity distributions. Due to the polarization-dependent VMs, the Xception model using multi-view data can provide faster training efficiency and excellent prediction accuracy. The correlation based on the DL-SPGD algorithm can be significantly increased to 99.997%, and the average correlation between the predicted and the measured VMs is 99.65%. The modal coefficients of the typical hybrid VVBs are quantitatively analyzed in the form of VM and OAM modal bases. Finally, the modal coefficients of high-order VMs using fiber MSCs demonstrate the experimental universality of the proposed MD method. This advancement not only bridges the gap between DL techniques and fiber optics but also promotes the precise characterization of VVBs in laser characterization, fiber MDM, and optical communications.