Geliang XU, Shiliang XING, Song YE, Jiaqi DENG, Man ZHANG. Reconfigurable and Storable Chaotic Logic Operations with the Performance of Error Detection and Correction[J]. Acta Photonica Sinica, 2023, 52(11): 1106004
- Acta Photonica Sinica
- Vol. 52, Issue 11, 1106004 (2023)
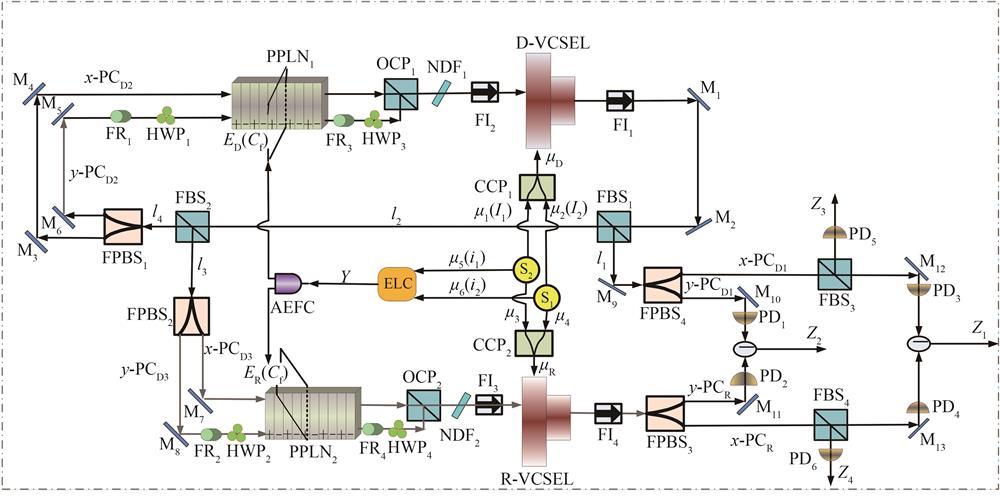
Fig. 1. The setup for chaotic system of drive-response VCSELs
Fig. 2. Dynamic state evolutions of polarized light x-PCD1，y-PCD1，x-PCR and y-PCR in the parameter space ED and μD
Fig. 3. Dynamic evolutions of the correlation function within the parameter space of the applied electric field and the normalized injection current
Fig. 4. The evolution curves of the correlation function with the change of the normalized injection current when the applied electric field is 0.434 3 kV/mm，0.583 kV/mm，0.73 kV/mm and 1 kV/mm
Fig. 5. Reconfigurable and storable chaotic logic OR，NAND，AND，XNOR，XOR and NOR operations
Fig. 6. Effect of noise strength D=1×109 on logic outputs Z1，Z2，Z3 and Z4
Fig. 7. Effect of noise strength D=1.77×109 on logic outputs Z1，Z2，Z3and Z4
Fig. 8. Effect of noise strength D=1.84×109 on logic outputs Z1，Z2，Z3 and Z4
Fig. 9. Effect of noise strength D=1.89×109 on logic outputs Z1，Z2，Z3 and Z4
Fig. 10. The evolution of the success probability P with the time delay τc
|
Table 1. Main system parameters
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 2. Maximum of the mean values of IDx（t）and IRx（t）for Cf=0 and minimum of the mean values of IDx（t）and IRx（t）for Cf=1 for different logic operations that Cf and the logic inputs satisfy
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 3. Maximum of the mean square errors of SEx and SEywhen Cf=0 and minimum of the mean square errors of SEx and SEy when Cf=1 for different logic operations that Cf and the logic inputs satisfy
Set citation alerts for the article
Please enter your email address
© Copyright 2018-2021 | Chinese Laser Press. All Rights Reserved 沪ICP备15018463号-20