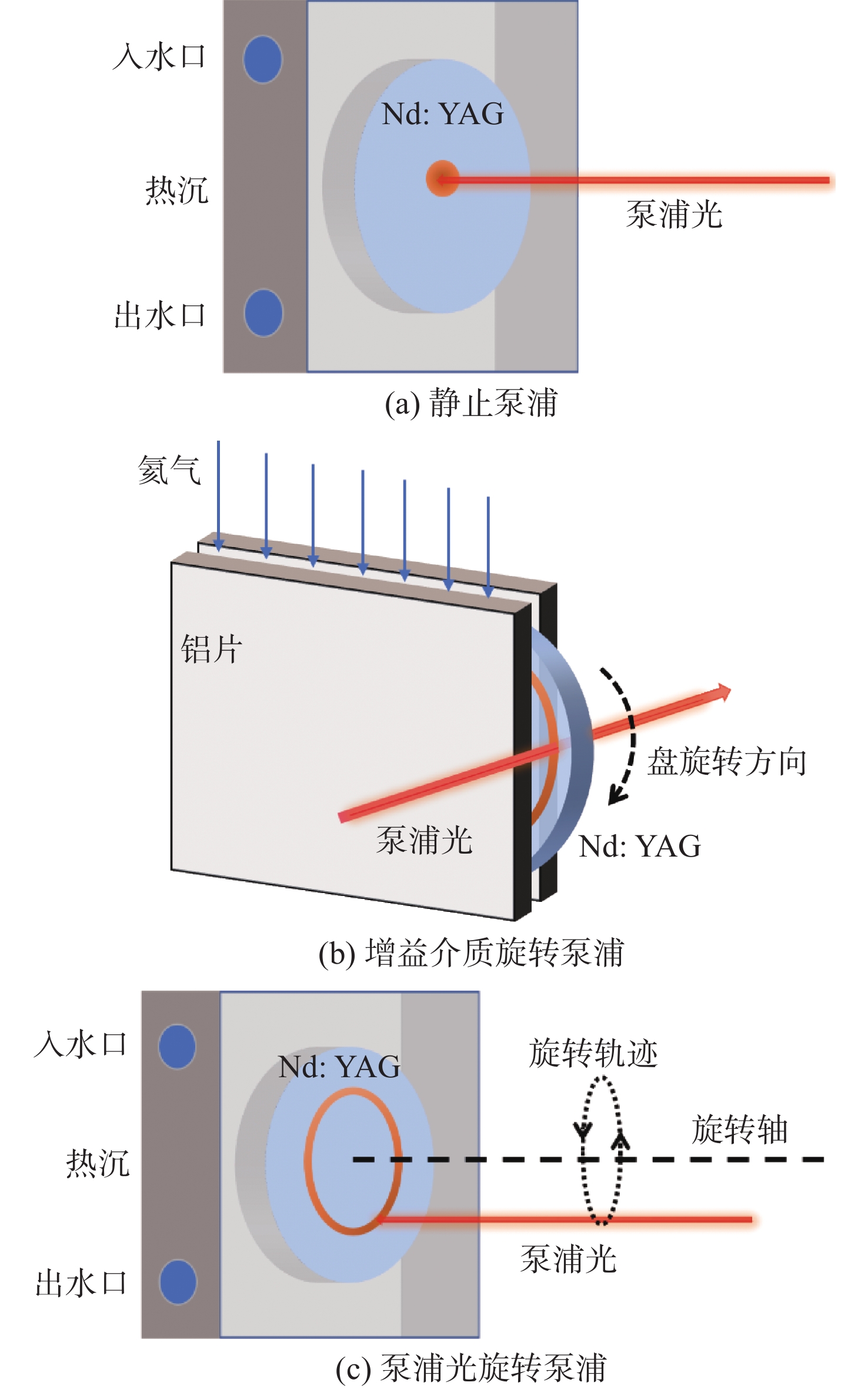
Bo ZHANG, Yuefei LI, Weilin CAO, Xiaojie HUANG, Dawei ZHANG, Jianlang LI. Research on Nd∶YAG solid-state laser with extracavity rotatory pumping[J]. Optical Instruments, 2024, 46(3): 87
Search by keywords or author
- Optical Instruments
- Vol. 46, Issue 3, 87 (2024)
Abstract
| (1) |
View in Article
| (2) |
View in Article
| (3) |
View in Article
| (4) |
View in Article
| (5) |
View in Article
Set citation alerts for the article
Please enter your email address



