Li-Jun Hu, Hai-Zhuan Yuan, Yu-Long Du. A modified HLLEM scheme and shock stability analysis [J]. Acta Physica Sinica, 2020, 69(13): 134701-1
- Acta Physica Sinica
- Vol. 69, Issue 13, 134701-1 (2020)
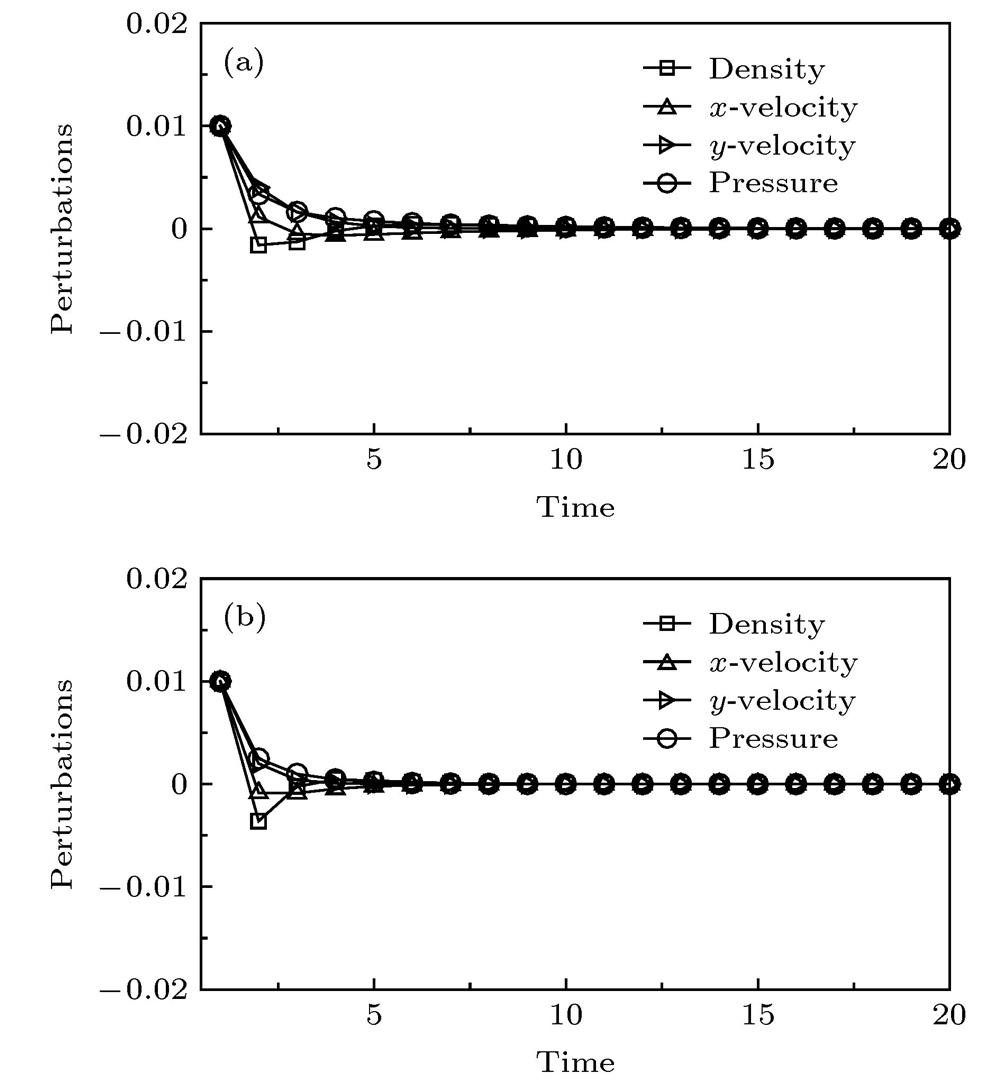
Fig. 1. Evolutionary curves of perturbation under supersonic condition: (a) Initial perturbation values and initial conditions (I); (b) initial perturbation values and initial conditions (II).
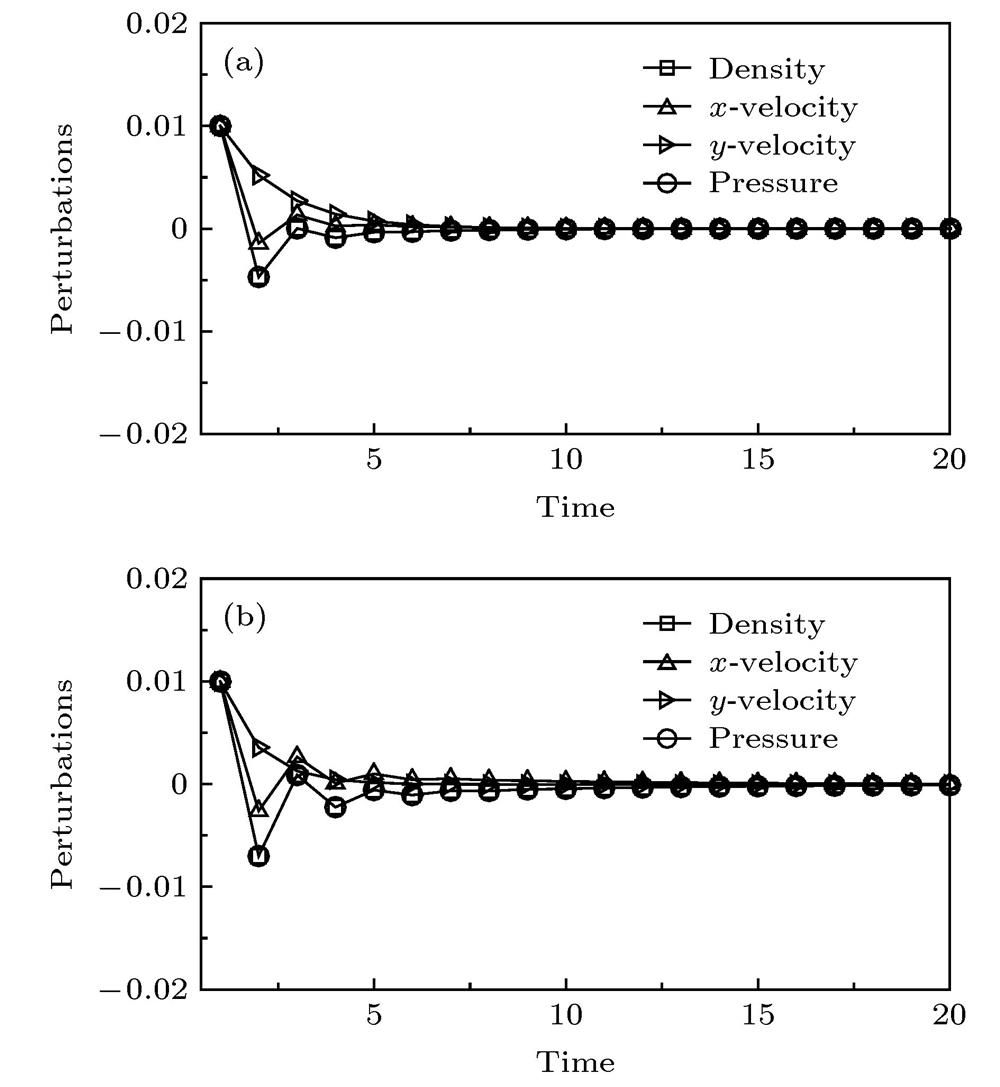
Fig. 2. Evolutionary curves of perturbation under subsonic condition: (a) Initial perturbation values and initial conditions (III); (b) initial perturbation values and initial conditions (IV).
Fig. 3. Evolutionary curves of perturbation in transverse direction: (a) Initial perturbation values (V); (b) initial perturbation values (VI); (c) initial perturbation values (VII); (d) initial perturbation values (VIII).
Fig. 4. Density contours for 2D Sedov blast wave problem: (a) HLLEM; (b) x -HLLE+y -HLLEM (c) x -HLLEM+y -HLLE.
Fig. 5. Curves for three different shock-detecting functions.
Fig. 6. Density contours of random numerical noise problem: (a) HLLEM; (b) M-HLLEM-g ; (c) M-HLLEM-g 1; (d) M-HLLEM-g 2.
Fig. 7. Maximum magnitude of velocity in y -direction of random numerical noise problem.
Fig. 8. Density contours of hypersonic flow over a cylinder: (a) HLLEM; (b) M-HLLEM.
Fig. 9. Density contours of double Mach reflection problem: (a) HLLEM; (b) M-HLLEM.
Fig. 10. Pressure contours of 2D Sedov blast wave problem: (a) HLLEM; (b) M-HLLEM.
Fig. 11. Density distribution of 2D inviscid contact discontinuity problem.
Set citation alerts for the article
Please enter your email address
© Copyright 2018-2021 | Chinese Laser Press. All Rights Reserved 沪ICP备15018463号-20