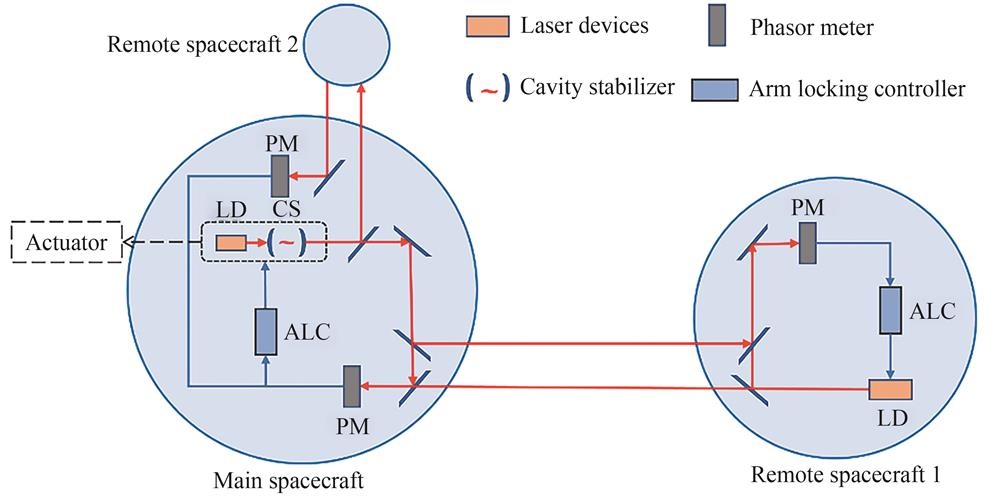
Shihao SU, Long MA, Xinyi ZHAO, Yongbin SHAO, Xutao YIN, Ming XIN. Design Method for Satellite-borne Single Arm Locking Controller Based on Bilayer Synchronized Optimization Strategy[J]. Acta Photonica Sinica, 2025, 54(2): 0254108
Search by keywords or author
- Acta Photonica Sinica
- Vol. 54, Issue 2, 0254108 (2025)
Note: This section is automatically generated by AI . The website and platform operators shall not be liable for any commercial or legal consequences arising from your use of AI generated content on this website. Please be aware of this.
Abstract
Set citation alerts for the article
Please enter your email address


 AI Video Guide
AI Video Guide  AI Picture Guide
AI Picture Guide AI One Sentence
AI One Sentence


