The rapidly developing quantum communication technology has had a profound impact on the field of information security. Quantum key distribution (QKD) is a key quantum communication technology based on the basic principles of quantum mechanics, which ensures secure key sharing between users while eavesdroppers cannot obtain the key information^[1,2]. Based on the physical quantities used for encoding, the QKD protocols can be divided into discrete-variable QKD (DV-QKD) and continuous-variable QKD (CV-QKD). CV-QKD does not require a single-photon light source or a single-photon detector, which makes it easier to implement. In CV-QKD, the key information is encoded on the quadrature components and decoded using coherent detection technology^[3–5]. As an important QKD protocol, CV-QKD has a high theoretical key rate within the metropolitan communication network range and is easily compatible with optical communication systems. Research on fiber-based CV-QKD has continued to advance, including high-rate point-to-point QKD^[6,7], QKD networks^[8–14], QKD hardware improvement^[15], and secure distance extension^[16–22].

In the current internet and global telecommunication networks, classical optical communications have been playing a critical role, achieving a transmission distance of more than 50,000 km^[23], a rate of more than 53.76 Tbit/s^[24], and providing support for more than thousands of nodes^[25]. This ensures high-rate information transmission between thousands of users. It is a current trend to combine classical and quantum communications. On the one hand, with the help of existing optical communication network infrastructure, it will be more cost-effective to deploy a QKD network. On the other hand, with QKD deployment, the security of data transmission of classical optical networks will be improved. However, there are also substantial differences between the two communication ways. The core difference is that the light intensity of classical communication is stronger, while the light intensity of the quantum signal is extremely weak. How to effectively integrate classical communication networks and quantum communication networks without affecting their respective performance has become a great challenge.

Currently, there have been many schemes to integrate classical and quantum communications. The commonly studied wavelength-division multiplexing (WDM) scheme can simultaneously transmit two or more optical signals of different wavelengths in the same optical fiber^[26]. It has a high transmission capacity and can save optical fiber resources. Meanwhile, WDM requires specialized equipment such as multiplexers and demultiplexers, which makes the maintenance of equipment costly and difficult. The time-division multiplexing (TDM) technology divides the time provided for the entire channel to transmit information into several time slots and allocates these time slots to each signal^[27]. This scheme is cheap and can be easily implemented. However, the disadvantage is that TDM is designed to work with a fixed number of channels and time slots, and it has limited flexibility and is unsuitable for high-speed networks. Another scheme for integrating classical and quantum communications is simultaneous quantum and classical communication, which can transmit both classical and quantum information in the same coherent state^[28,29]. However, classical communication in this scheme has a greater impact on quantum communication, and quantum communication has also become part of the noise in classical communication.

In this Letter, we proposed a scheme to realize classical communication and CV-QKD based on frequency-division multiplexing (FDM), and we verified the feasibility of simultaneously realizing a CV-QKD and classical optical communication data synchronous transmission scheme under the same infrastructure. FDM divides the total bandwidth into several non-overlapping frequency bands, allowing multiple signals of different frequencies to be simultaneously transmitted in the same optical fiber. This scheme can continuously transmit data compared with TDM and has higher bandwidth utilization. The disadvantage is that the frequency bands should be carefully selected to avoid crosstalk among different signals. Compared with the above schemes, FDM has higher bandwidth utilization and flexibility.

Quadrature phase shift keying (QPSK) is a digital modulation technique commonly used in optical communication systems. It is a phase modulation technique used to convert digital signals into analog signals for transmission. This technique employs two orthogonal carrier signals. Within each symbol period, two consecutive bits are shifted to a specific phase value. Typically, QPSK divides each phase into four different states, each state representing a combination of two bits, which means that QPSK can transmit two bits per symbol period, making it more efficient in terms of bandwidth utilization. Alice encodes information in a certain sequence of length $n$, and then modulates it on a coherent state with high average photon numbers. The $j$th signal can be expressed as $$|{\alpha }_c⟩=|A{e}^{i(2j+1)\pi /4}⟩,j\in \{0,\mathrm{1,}\dots ,n\},$$(1)where $A$ represents a strong optical amplitude and $i$ denotes the imaginary unit.

CV-QKD is a QKD protocol based on continuous-variable quantum states. CV-QKD can be divided into various protocols according to its modulation format, one of which is the Gaussian-modulated coherent state (GMCS) protocol. In the GMCS protocol, Gaussian distributed raw key data $\{x,p\}$ is modulated onto two orthogonal components of the coherent state. Alice modulates the key information on a coherent state $|x+ip⟩$, and Bob obtains the key information through a coherent receiver limited by shot noise.

In the modulation process, we modulate the baseband signal according to the corresponding carrier frequency of each signal. The in-phase component $y{a}_1$ and quadrature component $y{b}_1$ of the quantum signal can be expressed as $$\{\begin{array}{c}y{a}_1=a{s}_1\cos (2\pi f_{c}t)-b{s}_1\sin (2\pi f_{c}t)\\ y{b}_1=b{s}_1\cos (2\pi f_{c}t)+a{s}_1\sin (2\pi f_{c}t),\end{array}$$(2)where $a{s}_1$ and $b{s}_1$ are the original sequences, $f_c$ is the carrier frequency of the quantum signal, and $t$ is the time series. The modulated signal sent by Alice passes through the IQ modulator (IQM), variable optical attenuator (VOA), polarization modulator, beam splitter (BS), and optical isolator, and is finally received by Bob. When demodulating, we use coherent demodulation to remove the carrier wave and restore the baseband signal through phase recovery and balance compensation and to extract useful information from it. The quadrature components of the classical signal $y{a}_2$ and $y{b}_2$ can be expressed as $$\{\begin{array}{c}y{a}_2=a{s}_2\cos (2\pi f_{d}t)-b{s}_2\sin (2\pi f_{d}t)\\ y{b}_2=b{s}_2\cos (2\pi f_{d}t)+a{s}_2\sin (2\pi f_{d}t),\end{array}$$(3)where $a{s}_2$ and $b{s}_2$ are the original sequences, $f_d$ is the carrier frequency of the classical signal, and $t$ is the time series. The classical signal can be restored through the same process as the quantum signal. The amplitude of the classical signal is roughly dozens of that of the quantum signal.

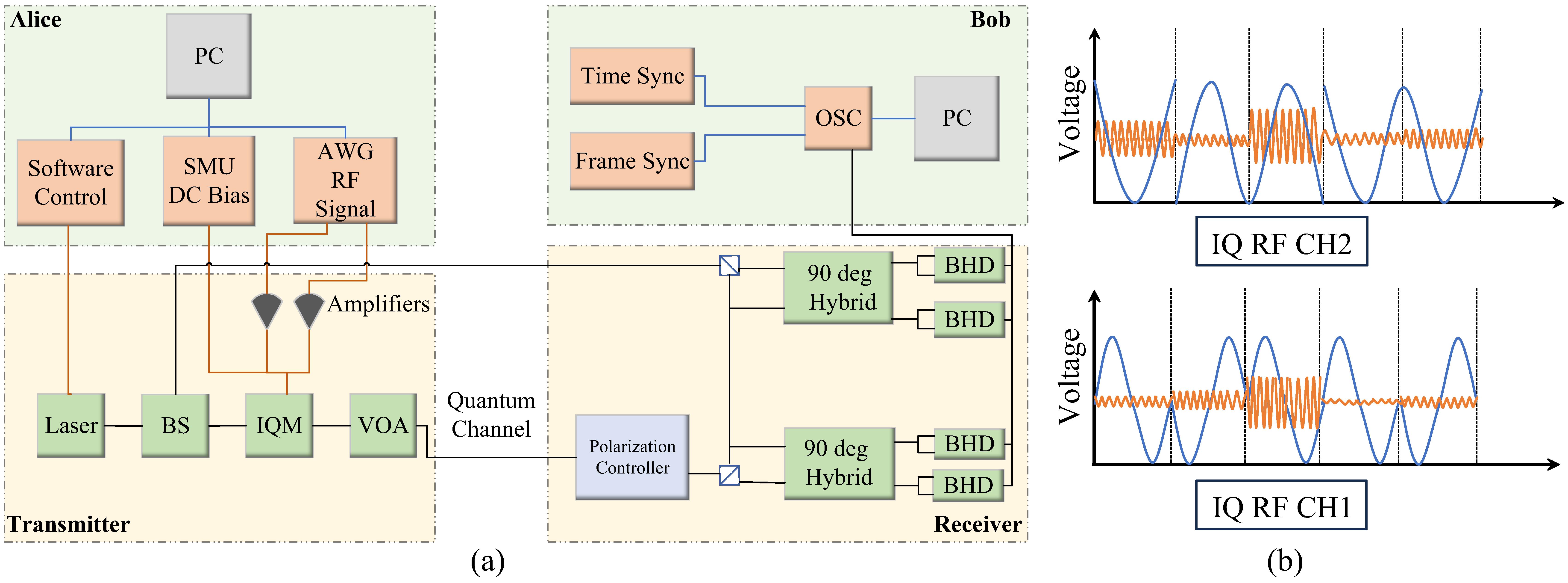
The structure of the experimental platform is shown in Fig. 1. At the transmitter, a 5 G/s high-speed arbitrary waveform generator (AWG) is used to load the electrical signal consisting of both the classical and the quantum parts, and a narrow linewidth laser is employed as the coherent state source of the quantum signal. An IQ modulator is then used to modulate the two quadrature components of the signal, with amplified AWG signals as one input and a DC bias calibrated by the feedback optical power as another input. The laser beam is split into two through a 1:99 beam splitter, between which the stronger one is directly guided to the receiver for coherent demodulation and the weaker one is modulated by the IQM. Finally, a VOA controls the output signal to a specific modulation variance $V_A$, which is set around 3.53 in the shot noise unit.

The polarization-diversity receiver module is made up of two optical hybrids and four coherent detectors, two of which act as quadrature component detectors while the other two are used to determine whether the polarization is aligned. The detected coherent state will then be converted into electrical signals at a sample rate of 2.5 G/s and transferred to the personal computer using a LAN cable. A manual polarization controller is employed for polarization management before the signal enters the receiver module. A 4 dB VOA simulates a 20 km quantum channel with a 0.2 dB/km loss. Using real optical fiber as the quantum channel will result in the same attenuation, but it will bring about more phase noise, which can be solved using recovery algorithms^[33]. The signal-to-noise ratio (SNR) of the classical signal is about 17.45 dB, an optical intensity within which the same coherent detectors can achieve good linearity detection.

As for signal modulation, two baseband signals are first generated with a 10 MHz repetition frequency. The first one, with voltages obeying the Gaussian distribution within 0 to 1, will later be modulated using the GMCS protocol, and the second one, with voltages obeying the binary distribution of $-1$ and 1, will later be modulated using the QPSK protocol. Based on the above scheme, we simulated the interference of classical signal sidebands on quantum signals under different frequency intervals and different amplitude ratios between classical signals and quantum signals. According to the simulation results, we choose a 500 MHz sinusoidal carrier for the GMCS signal and a 100 MHz sinusoidal carrier for the QPSK signal, with an amplitude ratio of 1:10. We then add the two modulated signals together to form a mixed signal, which will be loaded into the AWG for transmission. The chosen carrier frequency separates the two signals well in the frequency domain, and the chosen amplitude ratio ensures both signals work correctly, thus enabling Bob to perform coherent demodulation on the received signal and recover the original data through data processing.

Based on the above scheme, we simulated the interference of classical signal sidebands on quantum signals under different frequency intervals $\mathrm{\Delta }f=f_c-f_d$ and different amplitude ratios $n$ between classical signals and quantum signals. Since the filtering process is solving linear differential equations with constant coefficients, we used the Monte Carlo method to obtain the relation between frequency interval $\mathrm{\Delta }f$ and frequency division noise ${\epsilon }_F$ under different amplitude ratios $n$, as shown in Fig. 2. The noise ${\epsilon }_F$ is normalized using shot noise. Hollow points are obtained by the Monte Carlo method, and curves are obtained by nonlinear fitting. It can be seen from Fig. 2 that the noise ${\epsilon }_F$ between frequency bands is proportional to the square of the classical and quantum signal amplitude ratios $n$ and decreases as the frequency interval $\mathrm{\Delta }f$ increases. Interband noise ${\epsilon }_F$ can be expressed as $${\epsilon }_F=a{n}^2·\mathrm{\Delta }{f}^b,$$(4)where $a=9.432\times {10}^{99}$ and $b=-12.79$.

It can be seen that, on the one hand, as the intensity of the classical signal increases, the interference from the leakage of the classical signal will increase, leading to an increase in excess noise in the quantum channel. However, if the classical signal intensity is reduced, its own communication performance will be affected. On the other hand, as the frequency band between the two signals increases, its impact will gradually decrease. Therefore, while ensuring the performance of both signals, the larger the interval, the better the communication performance will be. When the frequency interval is over 300 MHz, the frequency cross-talk noise can be mostly ignored. So we have chosen 500 MHz as the carrier frequency of the quantum signal.

In data processing, a similar algorithm process is adopted for both the classical and quantum signals. First, the power spectrum of the signal is plotted to find out the frequency band range, after which coherent demodulation can be conducted to separate the classical signal and the quantum signal as well as the baseband signal and the carrier. After that, we use an appropriate digital filter to recover the basebands of both signals before we downsample them to the system symbol rate. We then implement the frame synchronization based on the cross-relation algorithm. Finally, phase compensation and balance compensation are conducted on the baseband signals. This is a crucial step as it corrects the phase drift during transmission and restores the orthogonality of the two quadrature components, which drift slightly during transmission due to the imperfection of the IQM. The phase compensation is based on a correlation method that finds the drifted phase by calculating the correlation between the two quadrature components and the original signal series with an angle variable multiplied to the expression. By changing the value of the angle variable, the correlation changes, and the angle variable value equals the drifted phase when the correlation reaches its maximum. During this process, a certain part of the key that only serves this purpose is disclosed, and it is not used to generate secret keys, therefore causing no problem for security. The balance compensation is based on Schmidt orthogonalization which orthogonalizes the two quadrature components. There is no frequency offset because the same laser is adopted as both the LO and the attenuator to simulate the channel. After recovery, ${10}^4$ samples of the quantum signal are disclosed to evaluate the excess noise and the channel transmittance^[30], and the same amount of samples of the classical signal are used to evaluate the bit error rate and bit rate. The achievable secret key rate (SKR) bound of the system is finally calculated according to Ref. [31], using a method that is asymptotic and does not take into account the finite-size effects. The formula can be expressed as $$R=f_{\mathrm{rep}}\times (1-a)(1-\mathrm{FER})(1-\nu )[\beta I_{\mathrm{AB}}-{\chi }_{\mathrm{BE}}].$$(5)

The relative experimental parameter values are shown in Table 1, and the specific formula details for CV-QKD can be obtained in Refs. [31,32].

Fifty data frames have been collected in the experiment, and the constellation diagram of the GMCS CV-QKD and the classical QPSK is shown in Fig. 3. The power spectrum diagram is shown in Fig. 4, on which we can see a substantial peak at 100 MHz, which is the QPSK signal, and then another smaller one at 500 MHz, which is the GMCS CV-QKD signal. There is also a peak at 0 MHz, which may be the $1/n$ noise caused by over sampling, and a peak at 200 MHz, which is likely to be the harmonic wave of the classical signal due to the imperfection of the carrier wave. Since the background noise shows a declining trend from 0 to 400 MHz and remains stable at higher frequencies, the smaller GMCS CV-QKD signal is placed at 500 MHz to minimize disturbance. The modulation variance $V_A$ of the GMCS signal is approximately 3.53 and the difference of power between the two signals is about 20 dB, indicating a 1:10 amplitude ratio between the carriers.

Figure 5(a) exhibits the excess noise and secret key rate through a 4 dB/km simulated channel of the GMCS CV-QKD signal in 50 frames, and Fig. 5(b) presents the bit error rate (BER) and bit rate of the classical QPSK signal. It is obvious that the BER of the classical signal stays at 0, and the bit rate stays at 10 Mb/s throughout the 50 frames. From Fig. 5(a), we can see that the excess noise of the quantum signal is kept under 0.1 SNU while the SKR stays above ${10}^5\text{bit}/\mathrm{s}$. The theoretical quantization noise in the analog-to-digital converter (ADC) and digital-to-analog converter (DAC) can reach $1.39\times {10}^{-4}$ SNU and $6\times {10}^{-4}$ SNU with 12 bit quantization and 10 bit quantization, respectively^[5]. Additionally, phase noise and modulation noise exert no influence in this experiment because phase compensation and balance compensation algorithms are implemented. Therefore, simultaneous transmission of both quantum and classical signals is made possible in the same infrastructure, making this method compatible with the classical software-defined network (SDN). This means that the transmission process of both signals can be controlled collectively through software, therefore making it more convenient and cost-efficient to perform further updates or maintenance.

We are aware that the excess noise of the quantum signal in this experiment is relatively higher compared with the TDM method^[27] where the quantum signal and the classical signal are transmitted separately in the channel. This is mainly due to the limited resolution of the DAC, affecting the accuracy of the output signal. Implementing a more sophisticated method to put the two signals together. Tuning the parameters of the IQM might address this issue. In addition, this scheme solves the issues of the precise control of time slots faced by TDM, which plays a good role in simplifying the system structure.

In this work, to the best of our knowledge, we have proposed the classical and quantum signals coexisting network system based on FDM for the first time and verified the feasibility of transmitting both signals simultaneously on different frequencies through experiments. We achieved a 0 bit error rate and a 20 Mb/s bit rate for the classical signal and an average secret key rate of around $5.86\times {10}^5\text{bit}/\mathrm{s}$ for the quantum signal through a 4 dB channel.

This scheme reveals the physical consistency between classic coherent optical communication and CV-QKD, and it also guides us to establish a QKD channel by only reserving a small passband in the entire optical communication instead of an entire wavelength, providing technical support for the construction of hybrid networks for both classical and quantum communications.