With the rapid development of atomic clocks, time-frequency has become a current physical quantity with the highest measurement accuracy^[1]. High-precision time-frequency signals play an important role in the fields of time-frequency comparison, basic physics research, and space exploration^[2–4], and these applications require high-precision time-frequency transfer systems. Current time-frequency transfer systems are mainly based on satellite links^[5,6], free-space optical links^[7,8] and fiber links^[9–11]. Due to the fiber advantages of low loss, strong anti-interference, and abundant resources, time-frequency transfer based on fiber links has become the main means of high-precision time-frequency transfer and has been widely studied. Fiber frequency transfer mainly includes microwave frequency transfer, optical frequency transfer, and optical frequency comb transfer, while microwave frequency transfer has a wide range of application prospects as it can be used directly by electronic devices. In 2018, the University of Western Australia achieved a 160 MHz frequency transfer of $9.7\times {10}^{-12}/\mathrm{s}$ and $3.9\times {10}^{-14}/1000\mathrm{s}$ over a 160 km fiber optic link^[12]. In 2023, the National Timing Center of the Chinese Academy of Sciences achieved a 10 GHz frequency transfer of $1.8\times {10}^{-14}/\mathrm{s}$ and $1.6\times {10}^{-17}/{10}^5\mathrm{s}$ over a 500 km cascaded fiber optic link^[13].

When using fiber links for frequency transfer, the light propagation path in the optical fiber changes due to the influence of external temperature changes. It leads to changes in the optical phase transmitted to the terminals, and thus causes a deterioration in the stability of the transmitted frequency. Therefore, a phase noise compensation device needs to be introduced into the fiber link to compensate for the phase noise due to temperature variations to achieve a high-precision frequency transfer. Traditional phase compensation methods include optical phase compensation and electrical phase compensation. Electrical phase compensation is susceptible to microwave leakage and has poor long-term stability. Optical phase compensation systems are large, small in compensation range, and not easy to industrialize. Therefore, starting from the fiber and finding the optical fiber that is not sensitive to temperature is an important direction for achieving fast, low-cost, and high-precision time-frequency transfer.

As a special fiber that has developed rapidly in recent years, the hollow-core photonic crystal fiber (HC-PCF) has many unique advantages over traditional solid-core fibers, such as low nonlinearity, low propagation delay, and temperature insensitivity^[14–17], due to transmission of light in the air core. According to the guiding mechanism, HC-PCF can be divided into the hollow-core photonic bandgap fiber and the hollow-core anti-resonant fiber. In 2015, the University of Southampton proved that the thermal coefficient of delay of the hollow-core photonic bandgap fiber was 2 ps km⁻¹ K⁻¹, which was an order of magnitude lower than that of the traditional solid-core fiber^[18]. In 2018, the team proved that zero propagation delay temperature sensitivity could be achieved in a hollow-core photonic bandgap fiber^[19]. Therefore, HC-PCF has a bright future in high-precision fiber time-frequency transfer.

In this article, we analyze factors that reduce the difficulty of fabrication by theoretically simulating the hollow-core anti-resonant fiber drawing process. The hollow-core anti-resonant fiber with a thicker outer nested tube wall is less sensitive to fluctuations in drawing conditions. By adjusting the wall thickness of the outer nested tube to a thicker value and using its second light conduction band, the difficulty of fabricating kilometer-length, low-loss hollow-core nested anti-resonant nodeless fibers is reduced. The lowest loss of the fabricated fiber is 2.7 dB/km at 1506 nm, and the bandwidth less than 5 dB/km is 1417–1620 nm. With the fiber loop optical-microwave phase discriminator system, we locked the 250 MHz repetition frequency of the optical frequency comb to a rubidium atomic clock. The thermal coefficient of delay for the fabricated hollow-core nested anti-resonant nodeless fiber is measured as 2.7 ps km⁻¹ K⁻¹, which is an order of magnitude lower than the 36.7 ps km⁻¹ K⁻¹ for the conventional single-mode fiber with the same length. We built a high-precision frequency transfer system using the prepared 1050 m hollow-core fiber, and the frequency stability is $1.67\times {10}^{-12}/\mathrm{s}$ and $5.66\times {10}^{-14}/1000\mathrm{s}$ when temperature changes over a wide range. It offers an order of magnitude of improvement in the frequency stability over the traditional single-mode fiber.

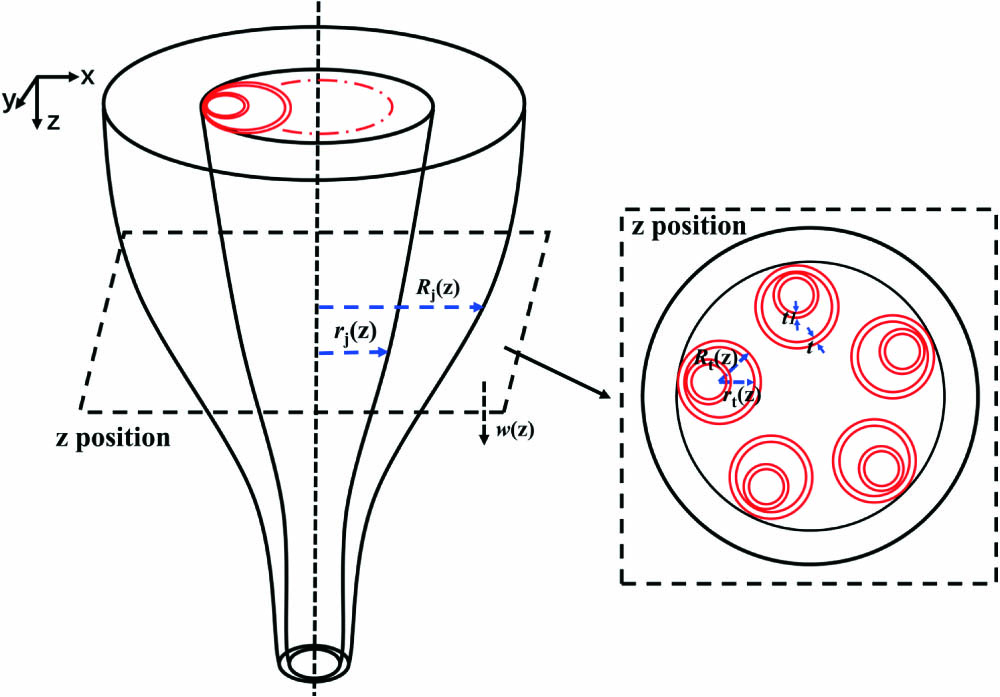
Hollow-core nested anti-resonant nodeless fibers (HC-NANFs) are prepared by the traditional two-stage stack-and-draw approach^[20]. First, several nested tubes are inserted into a jacketing tube with an outer diameter of 20–30 mm. The capillary tubes are fixed by molds at both ends so that the capillary tubes are closely tangent to the outer jacketing tube and form a preform. The preform is fused and scaled to a cane with an outer diameter of 3–6 mm. Next, the cane is assembled into a drawing tube and air chambers are formed in different areas of cane by specific molds. The stacking process in the first and second stages is completed in a clean room to avoid the contamination of preforms and the fiber breakage in the drawing of the long-distance hollow-core anti-resonant fiber. The hollow-core anti-resonant fibers of specific structures and sizes are drawn through the adjustment of the air pressure in the different air chambers. As the cladding of the hollow-core anti-resonant fiber consists of capillary tubes, the jacketing tubes bear the majority of the tension during the drawing process, and the tensile deformation of the capillary tubes is determined by the evolution of the jacketing tubes. Therefore, we can use the Fitt^[21] model to solve for the variation of the jacketing tube throughout the drawing process and use it as the boundary conditions to obtain the variation of the cladding capillary tube dimensions in the axial direction, which has been proved to be feasible in Ref. [22]. We add the cladding capillary tube dynamics equations to the Fitt model and obtain dynamic Eqs. (1)–(4) for hollow-core anti-resonant fiber drawing:$$(R_j^2-r_j^2)(w\frac{\mathrm{d}w}{\mathrm{d}z}-g)=\frac{\mathrm{d}}{\mathrm{d}z}(3\mu (R_j^2-r_j^2)\frac{\mathrm{d}w}{\mathrm{d}z}+\gamma (R_j+r_j)),$$(1)$$\frac{\mathrm{d}}{\mathrm{d}z}(R_j^{2}w)=\frac{\mathrm{d}}{\mathrm{d}z}(r_j^{2}w)=\frac{P_{\mathrm{core}}{R}_j^2{r}_j^2-\gamma R_j{r}_j(R_j+r_j)}{\mu (R_j^2-r_j^2)},$$(2)$$\frac{\mathrm{d}}{\mathrm{d}z}(R_t^{2}w)=\frac{\mathrm{d}}{\mathrm{d}z}(r_t^{2}w)=\frac{\mathrm{\Delta }P{R}_t^2{r}_t^2-\gamma R_t{r}_t(R_t+r_t)}{\mu (R_t^2-r_t^2)},$$(3)$$\frac{R_j^2-r_j^2}{2}(\rho c_{p}w\frac{\mathrm{d}T}{\mathrm{d}z}-\sigma \alpha (T_a^4-T^4))=R_j^{2}N(T_a-T),$$(4)where $R_j(z)$, $r_j(z)$, $R_t(z)$, $r_t(z)$ are the outer radius and the inner radius of the jacketing tube and the cladding outer capillary tube at position $z$, as illustrated in Fig. 1. $w(z)$ is the drawing speed at $z$. $P_{\text{core}}$ is the gas pressure applied in the jacketing tube, and $\mathrm{\Delta }P$ is the difference of the gas pressure applied in the jacketing tube and the outer cladding capillary tube. $g$ is the acceleration of gravity, $9.80665{\mathrm{m}/\mathrm{s}}^2$; $\rho$ is the density of the fused silica, $2200{\mathrm{kg}/\mathrm{m}}^3$; $\gamma$ is the surface tension of the fused silica, 0.3 N/m; $c_p$ is the specific heat, 1345 J/(kg K); and $\sigma$ is the Stefan–Boltzmann constant, $5.67\times {10}^{-8}\mathrm{W}/({\mathrm{m}}^2{\mathrm{K}}^4)$. $N$ is the heat transfer coefficient, $100\mathrm{W}/({\mathrm{m}}^2\mathrm{K})$, and $\alpha$ is the material radiation parameter, 0.885 m⁻¹. $T_a(z)$ and $T(z)$ are the furnace temperature distribution and silica temperature, respectively. By using the shooting method, we can solve Eqs. (1)–(4) based on the initial drawing conditions and target structure values.

In the actual drawing process, the gap between the cladding anti-resonant tubes needs to be controlled at a small distance to obtain a low loss, and small inhomogeneities in different anti-resonant tube sizes or positions increase the difficulty of controlling the fiber structure. Therefore, a large drawing tension is often required to control the fiber structure, which often leads to fiber breakage during drawing and thus makes it difficult to fabricate the long-distance hollow-core fiber. Due to the special light-guiding mechanism of the hollow-core anti-resonant fibers, we can choose different tube wall thicknesses and use different anti-resonant light-guiding bands to obtain low loss. We calculated the sensitivity of the nested outer tube wall thicknesses of 450 nm and 1150 nm to the initial preform nested tube size change and air pressure change according to the model we mentioned above. Figure 2(a) calculates the relationship between the fiber nested outer tube size and the preform nested outer tube size for the different wall thickness.

In our simulation, the same value is set for each condition of drawing, and the calculated tension is 265 g. We take the preform nested outer tube size of 6.2 mm and fiber nested outer tube size of 24.6 µm as reference. Due to different tube thicknesses, different air pressures need to be set in the calculation to achieve the target fiber nested outer tube size. The preform nested outer tube size is changed and brought into the simulation model to obtain the fiber nested outer tube size. We fitted the results to obtain the sensitivity of the fiber nested outer tube size to the preform nested outer tube size for the wall thickness of 450 nm and 1150 nm as 12.68 µm/mm and 7.0 µm/mm, respectively. The sensitivity of the fiber nested outer tube size to the change in gas pressure is calculated in Fig. 2(b). The pressure difference $\mathrm{\Delta }P$ is based on air pressure at the time of obtaining the fiber nested outer tube size of 24.6 µm from the preform nested outer tube size of 6.2 mm. The sensitivity of the fiber nested outer tube size to the gas pressure change is 3.38 µm/0.1 kPa and 0.08 µm/0.1 kPa for the wall thickness of 450 nm and 1150 nm, respectively. From the calculation results, we can see that the two sensitivities are reduced by twice and 40 times with thicker wall thickness. Therefore, the fiber structure can be better controlled at a lower tension, effectively reducing the difficulty of preparation.

We calculated the loss property of the five-ring nested anti-resonant nodeless fibers with different nested outer tube wall thicknesses using COMSOL. The wall thicknesses t1 of the nested inner tubes of the two fibers are both 450 nm. Figure 3 shows the calculated loss spectra, from which it can be seen that the fibers with 1150-nm-wall thickness and 450-nm-wall thickness have almost the same loss of 1 dB/km at 1550 nm. The available bandwidth of the fiber with 1150-nm thickness is 300 nm, which covers the spectral range of the optical frequency comb we use for the frequency transfer. Therefore, we chose 1150 nm as the target nested outer tube thickness to reduce fabrication difficulty, and we successfully prepared the kilometer-long low-loss hollow-core anti-resonant fibers under safe tension.

Figure 4(a) shows a scanning electron microscope (SEM) image of the cross section for our fabricated five-ring HC-NANF. The core diameter is 28 µm, and the thicknesses of the outer tube and nested tube are $1160\mathrm{nm}\pm 10\mathrm{nm}$ and $440\mathrm{nm}\pm 5\mathrm{nm}$, respectively. The loss was measured using the cut-back method and is shown in Fig. 4(b). In the cut-back measurement, we used a supercontinuum source (SC, YSL-SC-5 480–2200 nm) and an optical spectrum analyzer (OSA, Yokogawa, AQ6307C) to obtain the fiber transmission spectrum. The broadband light is butt-coupled to a hollow-core fiber through a single-mode fiber in a fiber fusion splicer (Furukawa, S178A, Japan), and the output of hollow-core fiber is connected to the OSA through a bare fiber adapter. To reduce the error in measurement, two cut-back measurements are performed in which the length of the fiber is cut from 1506 m to 3 m and from 1503 m to 3 m. Meanwhile, we cut the output end of the hollow-core fiber several times to obtain the best transmission spectrum and to avoid fluctuations in the coupling efficiency of light from the different lengths of the hollow-core fiber to the OSA. The loss results obtained from the two measurements are averaged and used as the fabricated fiber loss shown in Fig. 4(b). The low-loss bandwidth of less than 5 dB/km is 1417–1620 nm with a minimum loss of 2.7 dB/km at 1506 nm and 3 dB/km at 1550 nm. The inset of Fig. 4(b) is measured with a near-field camera image of the fabricated fiber output beam, which shows excellent beam quality. Additionally, we fused two single-mode fibers at each end of the fabricated fiber and used the $\phi$-OTDR system we built to measure its length. It can be seen from Fig. 4(c) that the two reflection peaks correspond to both ends of the hollow-core fiber, respectively, and the length of the fiber is calculated to be 1050 m.

Figure 5 shows a schematic diagram of the fiber loop optical-microwave phase discriminator (FLOM-PD) used to achieve the high-precision locking of the repetition frequency of a mode-locked laser to an atomic clock. A 10 MHz signal from a rubidium atomic clock is multiplied to generate a 1 GHz signal that serves as the microwave signal for the high-speed phase modulator of the FLOM-PD system, which consists of a Sagnac fiber loop, a phase modulator inside the loop, and a non-reciprocal $\pi /2$ phase shifter. Light from the mode-locked laser enters the fiber loop through a coupler. As the phase modulator is of the traveling-wave electrode type, it modulates only the light that travels in the same direction as the microwave signal propagation direction, and thus the light propagating clockwise and counterclockwise in the fiber loop produces a phase difference $\mathrm{\Delta }\phi$, which corresponds to the deviation of the optical frequency comb envelope pulse from the zero point of the microwave signal.

The non-reciprocal $\pi /2$ phase shifter in the loop consists of two Faraday rotators and a quarter-wave plate, which gives an additional $\pi /2$ phase difference between two directions of light and facilitates completion of the optical-microwave phase discrimination in an efficient linear region. The interference of light in both directions is detected by a detector and fed back to the piezoelectric ceramics after being processed by the PI circuit to control the cavity length of the laser in real time, thus realizing high-precision locking of the repetition frequency of the optical frequency comb with the atomic clock signal.

The optical fiber is affected by changes in the external environment (temperature, vibration) and propagation delay of light, resulting in the deterioration of the frequency transfer accuracy. In practical applications, the fiber link is inevitably affected by temperature changes in the environment during the day, and it has the greatest impact on the frequency transfer accuracy. Fiber propagation delay $\tau$ is expressed as$$\tau =\frac{n_g(T)L(T)}{c},$$(5)where $n_g$ is the group refractive index, $L$ is the fiber length, and $c$ is the speed of light in the vacuum. When the temperature changes, the propagation delay changes, $$\mathrm{\Delta }\tau =\frac{\mathrm{d}\tau }{\mathrm{d}T}\mathrm{\Delta }T=\mathrm{TCD}·L·\mathrm{\Delta }T,$$(6)where TCD represents the thermal coefficient of the fiber propagation delay. In the fiber links, the propagation delay $\tau (t)$, the phase change $\phi (t)$, the frequency change $\mathrm{\Delta }f(t)$, and the relative frequency change $y(t)$ have the relationship as follows: $$\phi (t)=2\pi f_0\tau (t),$$(7)$$\mathrm{\Delta }f(t)=\frac{\mathrm{d}\phi (t)}{2\pi \mathrm{d}t}=f_0\frac{\mathrm{d}\tau (t)}{\mathrm{d}t},$$(8)$$y(t)=\frac{\mathrm{\Delta }f}{f_0}=\frac{f_0\frac{\mathrm{d}\tau }{\mathrm{d}t}}{f_0}=\frac{\mathrm{d}\tau }{\mathrm{d}T}\frac{\mathrm{d}T}{\mathrm{d}t}.$$(9)

Therefore, the relative frequency change is mainly affected by two factors: the TCD and $\frac{\mathrm{d}T}{\mathrm{d}t}$. The Allan deviation ${\sigma }_y(\tau )$ is usually used to access frequency stability. When the environment temperature changes slowly, it is approximately regarded as a sine change $T(t)=T_0\sin (2\pi f_{T}t)$, and the Allan deviation can be calculated by the following equation:$${\sigma }_y(t)=\mathrm{TCD}·\frac{2L}{\tau }{\sin }^2(\pi f_T\tau ).$$(10)

Figure 6 shows the effect of the different TCD and temperature variation frequency $f_T$ on the fiber frequency transfer stability. It can be seen that the temperature variation has a small effect on the short-term stability of the frequency, but it worsens the long-term stability of the frequency. Frequency stability is worse at the half-period of the temperature change. The worse frequency stability is $2.31\times {10}^{-14}/6\mathrm{h}$ when the environmental temperature change period is 12 h and $1.1\times {10}^{-14}/12\mathrm{h}$ when environmental temperature change period is 24 h. Figure 6 also compares the effects of the different TCD on the frequency stability, from which the magnitude of the TCD affects the overall stability of the fiber frequency transfer. When the TCD increases by one order of magnitude from 10 ps km⁻¹ K⁻¹ to 100 ps km⁻¹ K⁻¹, the frequency stability changes from $1.1\times {10}^{-14}/12\mathrm{h}$ to $1.1\times {10}^{-13}/12\mathrm{h}$, and the overall frequency stability increases by one order of magnitude with the TCD.

After the above analysis of the temperature influence on fiber frequency transfer, we found that the fiber with the smaller TCD is an important direction to achieve a fast, low-cost, and high-precision time-frequency transmission. The TCD of an optical fiber can be expressed as$$\mathrm{TCD}=\frac{1}{L}\frac{\mathrm{d}\tau }{\mathrm{d}T}=\frac{1}{c}(\frac{\mathrm{d}{n}_g}{\mathrm{d}T}+\frac{1}{L}\frac{\mathrm{d}L}{\mathrm{d}T}{n}_g),$$(11)where $\frac{1}{L}\frac{\mathrm{d}L}{\mathrm{d}T}$ denotes the coefficient $\alpha$ of the fiber thermal expansion in the longitudinal direction ($5.5\times {10}^{-7}/\mathrm{K}$ for the conventional solid-core fibers when the fiber coatings are not considered). $\frac{\mathrm{d}{n}_g}{\mathrm{d}T}$ denotes the change of the refractive index with the temperature induced by the material thermo-optic effect (silica $\frac{\mathrm{d}{n}_g}{\mathrm{d}T}=1.1\times {10}^{-5}/\mathrm{K}$ at 1550 nm). The TCD for the conventional solid-core fibers is therefore 39 ps km⁻¹ K⁻¹. In the hollow-core fibers, most of the light is confined in the air core. It allows the $\frac{\mathrm{d}{n}_g}{\mathrm{d}T}$ term in the TCD to be neglected, and there is only a change in time delay due to the fiber thermal expansion in the longitudinal direction. We constructed a two-dimensional computational model of COMSOL based on the SEM of the fabricated HC-NANF to compute its TCD. In the computation, the initial temperature is set to 25°C, and the refractive index at each temperature is set according to the thermo-optic coefficient of the silica. The dispersion curve of the fundamental mode is calculated to obtained $n_g$, which is linearly fitted to the temperature to obtain $\frac{\mathrm{d}{n}_g}{\mathrm{d}T}$.

Figure 7 shows the theoretically calculated TCD curve of the hollow-core fiber used in the experiment and the contribution curves of the longitudinal thermal expansion effect and the thermo-optical effect to the TCD, respectively. It can be seen that most of the light energy is bound in the air core, the thermo-optic effect of silica is neglected in the low-loss bandwidth, and only the longitudinal thermal expansion contributes to the TCD, which is of the magnitude of 2 ps km⁻¹ K⁻¹. It is an order of magnitude lower than that of the conventional solid-core fiber. Therefore, hollow core fibers have potential applications for fast, low-cost, high-precision fiber frequency transfer.

Figure 8 is a diagram of the experimental setup for measuring the TCD of the HC-NANF and the single-mode fiber. An optical frequency comb with a repetition frequency of 250 MHz locked on the rubidium atomic clock passes through the 1:9 coupler. One path is detected by the photodetector after passing through 1050 m fabricated HC-NANF placed in the temperature control box, and the other path is detected directly by the photodetector as a reference optical path. The signal frequency detected by the photodetector consists of a repetition frequency of 250 MHz and its octave. In order to better compare the difference between the two paths, we selected a 500 MHz signal as the comparison frequency. In the experiment, we gradually increase the temperature from 0°C to 40°C and use a signal acquisition card to record the voltage change curve, from which we can calculate the change of the phase difference between the two paths with temperature.

Figure 9 shows the experimentally measured change in the phase difference of the two paths with time. It can be seen that when the temperature increases from 0°C to 40°C, the phase difference between the two paths increases from 0.87 rad to 1.22 rad. As the temperature increases, the time delay of the optical frequency comb through the NANF increases and thus results in the phase difference between the two paths of the light changes by 0.35 rad. Using equation $\mathrm{\Delta }\phi =2\pi f_0\mathrm{\Delta }\tau$, we can obtain the time delay difference change $\mathrm{\Delta }\tau$ according to the phase difference change. $f_0$ is 500 MHz selected for the experiment, and the delay difference due to temperature change is calculated to be 113 ps. According to Eq. (6), the TCD of the NANF used in this experiment is 2.7 ps km⁻¹ K⁻¹. Repeat the above experiments by replacing the NANF with the same length of single-mode fiber. The phase difference and delay difference caused by the temperature change are 4.74 rad and 1510 ps, respectively, and the TCD of the SMF is calculated to be 36.7 ps km⁻¹ K⁻¹.

Figure 10 shows an optical frequency comb transfer system based on the fabricated HC-NANF. The system consists of three parts: frequency locking, frequency transfer, and frequency measurement and evaluation.

A femtosecond mode-locked laser with a repetition frequency of 250 MHz is split into two paths through a fiber coupler. One path passes through the FLOM-PD device to realize the locking of the repetition frequency to the atomic clock, while the other path is used for the frequency transfer. The signal generated by the rubidium atomic clock is multiplied by a frequency multiplier to generate a 1 GHz microwave signal into the FLOM-PD, which completes the phase identification between the optical pulse signal and the microwave signal and passes the error signal to the PZT to control the cavity length of the mode-locked laser. It realizes the locking of the microwave signal of the rubidium atomic clock to the repetition frequency of the optical frequency comb. The optical pulse carrying the microwave reference signal passes through the 1050 m fabricated NANF link for the frequency transfer. The repetition frequency is directly detected by the photodetector and collected by the high-precision frequency counter.

Due to the limitation of the length of the experimental fiber, we set the temperature variation range to 40°C to simulate the long-distance fiber frequency transfer. The 1050 m NANF is put into the temperature control box and the temperature is increased from 0°C to 40°C with a set time of 1 hour and then lowered to 0°C with a set time of 1 hour as well. The time of the periodic temperature change is 2 hours, and the frequency jitter is collected by a frequency counter. As shown in Fig. 11(a), the transmitted optical frequency comb repetition frequency jitter range is 2 mHz during the whole temperature change process. To further evaluate the performance of the frequency transfer system, we use the Allan deviation to characterize the frequency stability. The red curve in Fig. 11(b) shows the stability of the frequency transfer system based on the fabricated NANF, which can reach $1.67\times {10}^{-12}/\mathrm{s}$ and $5.66\times {10}^{-14}/1000\mathrm{s}$ when the temperature undergoes a wide range of variation. In order to compare the advantages of the hollow-core fiber, we replaced the experimental NANF with the SMF of the same length and repeated the above experiments. The black curve in Fig. 11(b) shows the frequency stability obtained by replacing the NANF with the SMF of the same length, and the frequency stability can reach $1.65\times {10}^{-12}/\mathrm{s}$ and $5.27\times {10}^{-13}/1000\mathrm{s}$.

Based on the experimentally measured TCD values and formula ${\sigma }_y(\tau )=\mathrm{TCD}·\frac{2L}{\tau }T{\sin }^2(\pi f_T\tau )$, we theoretically calculated the change in the frequency stability due to the temperature change, and the results are shown in Fig. 12. The blue curve in Fig. 12 represents the experimentally measured frequency stability without the fiber link. It can be seen that as the temperature changes slowly, the short-term stability of the frequency transfer is not affected by the temperature change and is mainly limited by the stability of the atomic clock. However, the long-term stability of the frequency, especially at the half-period of the temperature change, deteriorates. The TCD of the NANF is 2.7 ps km⁻¹ K⁻¹, which allows the stability of the frequency transfer system to reach $5.1\times {10}^{-14}/1000\mathrm{s}$, which is an order of magnitude higher than that of the single-mode fiber of $6\times {10}^{-13}/1000\mathrm{s}$. It is basically consistent with our experimentally measured results. Therefore, we have achieved fast, efficient, and low-cost frequency transfer using the NANF links when the temperature changes.

By improving the structural design of the hollow-core anti-resonant fiber, we have reduced the difficulty of preparing long-distance low-loss hollow-core anti-resonant fibers, and successfully fabricated a 1050 m high-performance hollow-core nested anti-resonant nodeless fiber with a minimum loss of 2.7 dB/km at 1506 nm and more than 200 nm bandwidth below 5 dB/km. We investigated the effect of the temperature on the frequency transfer of the fiber links, and theoretically analyzed and calculated thermal sensitivity of the propagation delay of hollow-core anti-resonant fibers. Experimentally, an optical frequency comb with 250 MHz repetition frequency is locked to a rubidium atomic clock by the FLOM-PD system. A high-precision frequency transfer system is accomplished through the fabricated hollow-core fiber, and the frequency stability can reach $1.67\times {10}^{-12}/\mathrm{s}$ and $5.66\times {10}^{-14}/1000\mathrm{s}$. The excellent characteristics of the hollow-core anti-resonant fiber used for the frequency transfer are measured and verified. The TCD of the fabricated HC-NANF was experimentally measured to be 2.7 ps km⁻¹ K⁻¹, which is an order of magnitude lower than that of the single-mode fiber of 36.7 ps km⁻¹ K⁻¹ with the same length. This results in a frequency transfer stability of $5.66\times {10}^{-14}/1000\mathrm{s}$ for the NANF link when the temperature varies, which is nearly an order of magnitude lower than the $5.27\times {10}^{-13}/1000\mathrm{s}$ for the single-mode fiber. Therefore, we realized a fast, efficient, and cost-effective high-precision frequency transfer based on the NANF without any compensation device.