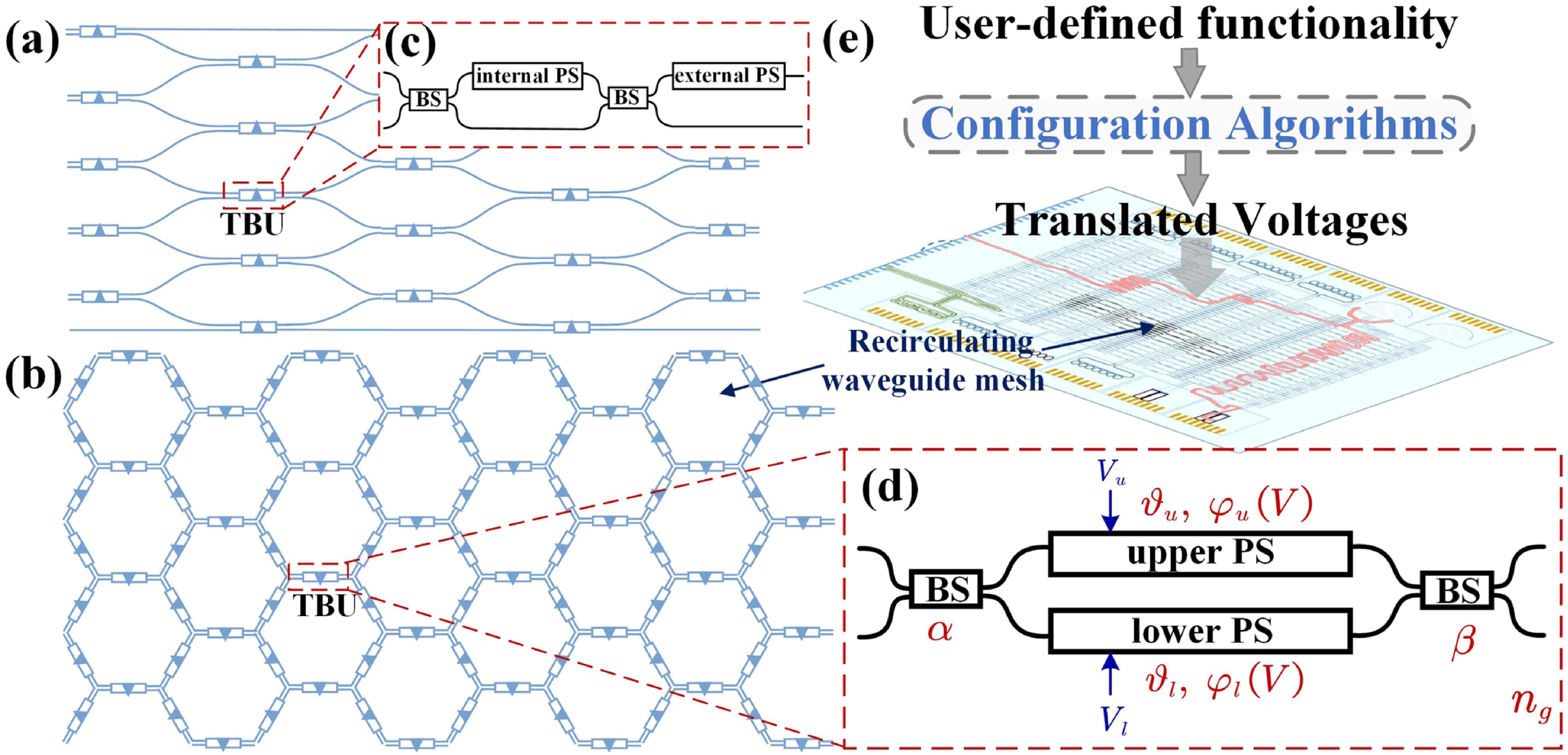
Programmable photonic integrated circuits (PPICs)^[1–4], as an alternative to application-specific photonic integrated circuits (ASPICs), enable various functionalities to be configured on the same waveguide mesh. Such waveguide meshes are built from many tunable basic units (TBUs) connected based on 2D fixed topologies, as shown in Figs. 1(a) and 1(b). Based on whether they support light backward propagation, waveguide meshes can be divided into two categories: 1) feedforward-only waveguide meshes^[3,5] [as shown in Fig. 1(a)], which support only feedforward light propagation and are often used to configure multiport interferometers; 2) recirculating waveguide meshes [as shown in Fig. 1(b)], which support both feedforward and feedback light propagation, thereby offering enhanced functional versatility and can be used to configure both finite and infinite multiport interferometers and filters^[3,5,6]. While the complex structure of recirculating waveguide meshes provides great functional flexibility, it simultaneously poses great challenges in practical applications.

As shown in Fig. 1(e), the programming of PPIC relies on configuration algorithms to translate user-defined functionalities into voltages applied to waveguide meshes^[2,7–13]. However, imperfections introduced during fabrication can degrade the performance of these algorithms, as the voltages retrieved based on an ideal assumption may not suit the actual fabricated mesh^[14,15]. Attempts have been made to solve this problem by running these algorithms in an on-chip manner, using the measurement results of the fabricated mesh as feedback for these algorithms to ensure suitability for the actual defective mesh^[7,8,16,17]. This approach is effective but inefficient^[8,9,18], as it typically involves a number of time-consuming tasks of setting and measuring the mesh^[18]. A better solution would be to adopt an off-chip manner, using simulation methods^[15,19–21] and analytical gradient calculation methods^[20,21] to build a virtual model of the fabricated mesh and replace the actual measurement of the fabricated mesh with analytical calculations. This improves efficiency but relies on accurate characterization of the fabricated mesh to ensure proper alignment.

However, characterizing recirculating waveguide meshes is particularly challenging. The more complex topology [Fig. 1(b)] and compact TBU structure [Fig. 1(d)] of the recirculating waveguide meshes, while offering more flexible functionality, also make their characterization difficult. Additionally, the flexibility required by such meshes also poses a higher characterization demand. These complexities make the characterization methods suitable for feedforward-only waveguide meshes^[23,24] neither applicable nor sufficient. Also, existing methods suitable for recirculating waveguide meshes have been limited to primarily focus on characterizing only certain parameters^[16,18,25], which is not sufficient for use in simulation methods or analytical gradient calculation methods, making it inadequate when it comes to the practical application of off-chip configuration. Therefore, in this Letter, we propose a new characterization method suitable for recirculating waveguide meshes.

Our method utilizes an optimization method to infer the imperfection parameters from the test result of the actual fabricated mesh. We also design a step-by-step procedure that can narrow down the possible range of certain imperfection parameters before the optimization, helping to reduce the parameter space and providing a good starting position for optimization. With this technique, the range of parameters that can be characterized is greatly broadened compared to existing methods, making it sufficient for use in simulation methods and analytical gradient calculation methods (see Sec. S1 in the Supplementary Material for detailed comparison). To demonstrate the effectiveness of our method in precise characterization, we used the characterized parameters to build a model of the detective mesh and demonstrate its ability to accurately predict the mesh transmission matrices. Moreover, we carried out our method under various scenarios to analyze its stability and robustness. Lastly, we applied our method to the implementation of six different kinds of finite/infinite impulse response (FIR/IIR) filters to demonstrate the effectiveness of our method in configuring applications on defective meshes.

In recirculating waveguide meshes [Fig. 1(b)], TBUs [Fig. 1(d)] are implemented with a symmetric Mach–Zender interferometer (MZI) composed of 50:50 beam splitters (BSs) and phase shifters (PSs) attached to both arms. As mentioned earlier, the flexibility required by the recirculating waveguide meshes poses higher characterization demand. For such meshes, their applications in configuring filters necessitate their performance being evaluated across the entire frequency band, rather than at a single frequency point. Furthermore, the actual phases of each PS on both TBU arms must be obtained, rather than just the phase difference between the upper and lower arms, as in feedforward meshes. Thus, recirculating waveguide meshes requires a more comprehensive model that considers more imperfection factors. Therefore, our modeling considers various fabrication imperfections, including the passive phase without the voltage applied (${\vartheta }_u$ and ${\vartheta }_l$) and the phase increment versus the voltage [${\phi }_u(V)$ and ${\phi }_l(V)$] of the upper and lower PSs, the splitting ratio of the BSs ($\alpha$ and $\beta$), and the group index of the waveguide ($n_g$). Due to fabrication errors, the actual values of these parameters may deviate from the ideal ones. With the actual values known, a virtual model of the fabricated mesh can be built, as discussed in Sec. S2 in the Supplementary Material.

Thus, our characterization method aims to characterize these imperfections of each TBU in the mesh, i.e., ${\mathit{C}}_{\mathit{p}}=\{{\overrightarrow{\vartheta }}_u,{\overrightarrow{\vartheta }}_l,{\overrightarrow{\phi }}_u(V),{\overrightarrow{\phi }}_l(V),\overrightarrow{\alpha },\overrightarrow{\beta },{\overrightarrow{n}}_g\}$ (→ indicates vectors composed of the corresponding parameters of each TBU).

Existing methods suitable for recirculating waveguide meshes have been limited to primarily focus on characterizing only certain parameters, such as the coupling factor of the TBU versus the applied voltage or required voltage to set the TBU to the cross/bar state^[16,18,25]. However, this is insufficient for use in simulation methods or analytical gradient calculation methods, as the working principle of these methods requires the specific imperfection parameters of each component of the TBU, rather than just the resultant coupling factor. Therefore, to enable the practical use of these methods in off-chip configuration, all parameters in ${\mathit{C}}_{\mathit{p}}=\{{\overrightarrow{\vartheta }}_u,{\overrightarrow{\vartheta }}_l,{\overrightarrow{\phi }}_u(V),{\overrightarrow{\phi }}_l(V),\overrightarrow{\alpha },\overrightarrow{\beta },{\overrightarrow{n}}_g\}$ will need to be characterized. To handle such a wide range of imperfection parameters, we design a step-by-step procedure to gradually narrow down the possible value ranges of the parameters, followed by an optimization method that ultimately determines their values. The characterization procedure comprises 4 steps (the function of each step is illustrated in Fig. 2), outlined as follows:

Step 1: Characterization of $d\overrightarrow{\vartheta }={\overrightarrow{\vartheta }}_l-{\overrightarrow{\vartheta }}_u$, ${\overrightarrow{\phi }}_u(V)$ and ${\overrightarrow{\phi }}_l(V)$

Using the method proposed in Ref. [25], we can have the coupling factor of the TBU relative to the applied voltages ($V$). $d\overrightarrow{\vartheta }={\overrightarrow{\vartheta }}_l-{\overrightarrow{\vartheta }}_u$, ${\overrightarrow{\phi }}_u(V)$ and ${\overrightarrow{\phi }}_l(V)$ are then retrieved from the coupling factor. The detailed principle is discussed in Sec. S3 in the Supplementary Material.

Step 2: Characterization of ${\overrightarrow{n}}_g$

Our characterization method includes characterizing the group index $n_g$ of the waveguide to allow for performance evaluation across the entire frequency band. $n_g$ is characterized by synthesizing a MZI resonator on the mesh, and then deducing it from the free spectral range (FSR)^[26] of the MZI resonance spectrum^[27,28]. The detailed principle of ${\overrightarrow{n}}_g$ characterization is discussed in Sec. S4 in the Supplementary Material.

Step 3: Narrowing down the value ranges of ${\overrightarrow{\vartheta }}_u$ and ${\overrightarrow{\vartheta }}_l$

The phases of each PS on both arms of the TBU need to be characterized. However, these phases cannot be easily obtained because, in recirculating waveguide mesh, the formation of interference requires the participation of multiple TBUs, making it impossible to separate the effects of different TBUs. Consequently, deducing the phase information of the PS from the interference light intensity, a task that can be easily done in characterizing feedforward-only waveguide meshes, becomes infeasible. Without the phase information, the passive phase could potentially span any value between 0 and $2\pi$, thus complicating the characterization process due to the broad search range. Therefore, here we propose a novel method, capable of narrowing down the value range of the passive phase of the PS (${\vartheta }_{u/l}$) to two potential values. The detailed principle is discussed in Sec. S5 in the Supplementary Material.

Step 4: Characterizing utilizing optimization

In the final step of our characterization routine, we utilize an optimization method to find the optimal value of ${\mathit{C}}_{\mathit{p}}$ based on the criterion of making the mesh behavior closely resemble that of the fabricated one. After the previous three steps, some parameters in ${\mathit{C}}_{\mathit{p}}$ have already been characterized or have their potential value ranges narrowed down. Thus, in Step 4, the optimization is simplified with a reduced parameter space. The detailed principle is discussed in Sec. S6 in the Supplementary Material.

Next, simulation verification of our method is conducted on a waveguide mesh containing 36 TBUs. In order to verify the effectiveness of our method, we conduct 30 experiments by randomly generating ${\mathit{C}}_{\mathit{p}}$ (see Sec. S7 in the Supplementary Material), then use the proposed characterization method to retrieve them. In the final step of our characterization procedure, the optimization process requires measurement data of the fabricated mesh. This data is obtained by measuring the mesh transmission matrix under 45 different sets of the randomly chosen voltage settings, at a single frequency point. To evaluate the effectiveness of the proposed method, the characterized imperfection values are compared with the actual values to calculate the characterization errors. The probability density function (PDF) of the characterization error of $K_{\mathrm{BS}}$ (BS splitting ratio) is shown in Fig. 3(a), indicating that the proposed method can ensure characterizing $K_{\mathrm{BS}}$ with an error less than 1.34% in 95% of the cases. The PDF of characterization error of $d\vartheta ={\vartheta }_l-{\vartheta }_u$ is shown in Fig. 3(b), indicating that the proposed method can ensure characterizing $d\vartheta$ with an error smaller than $0.0026\pi$ in 95% of the cases. Also, to evaluate the effectiveness of our method in ensuring accurate modeling of the actual mesh, a virtual model of the mesh is built using the characterized value ${\widehat{\mathit{C}}}_{\mathit{p}}$. Under 100 different sets of randomly generate voltage settings, the corresponding mesh transmission matrix (in dB) is predicted using this model. The predicted transmission matrices ($\widehat{\mathit{T}}$) are then compared with those of the actual mesh ($\mathit{T}$) to calculate the transmission matrix prediction error. Notably, since recirculating waveguide meshes are often used to configure filters, it is important to evaluate the proposed method’s performance over the entire frequency band. Thus, when calculating the transmission matrix prediction error, the errors are calculated at $N_f=50$ frequency points across the whole FSR (corresponding to the length of a single TBU), rather than at a single frequency point. The PDF of the prediction error is shown in Fig. 3(c), indicating that the proposed method can ensure accurate prediction of transmission matrices with an error less than 0.55 dB for 85% of the cases. The PDFs, along with error ranges and corresponding confidence levels of the characterization errors of $K_{\mathrm{BS}}$ and $d\vartheta$ and the prediction error of $\mathit{T}$ are summarized in Fig. 3.

We also adopt the root mean square error (RMSE) [Eq. (1)] to measure the average prediction error of the transmission matrices. In our case, the average RMSE over 30 experiments is 0.35 dB, $$\mathrm{RMSE}=\sqrt{\frac{{\sum }_{l=1}^{N_{\mathit{V}}}{\sum }_{k=1}^{N_f}{\sum }_{j=1}^{N_{\text{port}}}{\sum }_{i=1}^{N_{\text{port}}}{[10\lg ({\widehat{t}}_{i,j,k}^{(l)})-10\lg (t_{i,j,k}^{(l)})]}^2}{N_{\text{port}}^2·N_{\mathit{V}}·N_f}},$$(1)where $t_{i,j,k}^{(l)}$ and ${\widehat{t}}_{i,j,k}^{(l)}$ are the weights of ${\mathit{T}}^{(l)}$ and ${\widehat{\mathit{T}}}^{(l)}$, and ${\mathit{T}}^{(l)}$ and ${\widehat{\mathit{T}}}^{(l)}$, respectively, are the predicted transmission matrix and the actual one. The superscript $l$ denotes the index for a particular voltage setting, and $N_{\mathit{V}}$ is the total number of voltage settings. The subscripts $i,j$, and $k$ represent the row, column, and spectral slice index of a certain weight, respectively. $N_{\text{port}}$ is the number of ports of the waveguide mesh, determining the row and column count of ${\mathit{T}}^{(l)}$, and $N_f$ refers to the spectral slice count of ${\mathit{T}}^{(l)}$, i.e., the number of frequency points at which the mesh transmission matrices are measured.

Evidently, even though our characterization procedure was conducted at a single frequency point, it can precisely predict the transmission matrices over the entire FSR. Overall, we have demonstrated that the proposed method can characterize imperfections precisely and ensure accurate modeling of the defective mesh.

To further analyze the stability and robustness of the proposed method, we tested it under various real-world scenarios, considering different BS splitting ratio variances, inaccurate measurements of the mesh, inaccurate TBU insertion loss characterization, and inaccurate voltage control.

First, we consider differnt BS splitting ratio ($K_{\mathrm{BS}}$) variances, assuming $K_{\mathrm{BS}}$ follows a Gaussian distribution with a standard deviation of ${\sigma }_{\mathrm{BS}}$ (a typical wafer-level $K_{\mathrm{BS}}$ variation is ${\sigma }_{\mathrm{BS}}=2\%$)^[29]. Second, we consider the measurement inaccuracies when measuring the transmission matrices $\mathit{T}$ of the fabricated mesh. The inaccuracy is simulated by introducing random fluctuations to the accurate $\mathit{T}$, where the magnitude of fluctuations follows a Gaussian distribution with a standard deviation of ${\sigma }_{\mathit{T}}$. Third, we consider inaccuracies in the TBU insertion loss (IL) characterization. The IL of the TBU can be characterized using the method outlined in Ref. [18], and, when characterized correctly, it does not affect the proposed method’s performance in characterizing ${\mathit{C}}_{\mathit{p}}$. However, acknowledging potential inaccuracies in the IL characterization, as described in Ref. [18], where the average IL characterization error is 0.18 dB, we also tested the proposed method in the presence of inaccurate IL characterization. The IL characterization inaccuracy is simulated by introducing errors to the actual IL, where the errors follow a uniform distribution with an absolute average of ${\mu }_{\mathrm{IL},e}$. We demonstrated that the proposed method showed strong robustness under various practical scenarios, exhibiting an average RMSE of 0.8 dB under the circumstance of ${\sigma }_{\mathrm{BS}}=2.5\%$, ${\sigma }_{\mathit{T}}=5\%$, and ${\mu }_{\mathrm{IL},e}=0.2\mathrm{dB}$. Last, we examined the impact of inaccurate voltage control by testing our method under various digital-to-analog converter (DAC) bit resolutions and found that the proposed method required a DAC resolution greater than six bits. A detailed performance analysis under different scenarios is discussed in Sec. S8 in the Supplementary Material.

Lastly, we demonstrate the effectiveness of our characterization method through the implementation of FIR filter applications, including two MZIs with different arm length differences and a 3-tap MZI lattice filter, as shown in Figs. 4(a)–4(c).

We first configured the filters using voltages chosen based on an ideal assumption. As a result, the normalized spectral responses of an ideal mesh, the actual mesh, and the characterized mesh were plotted in Figs. 4(d)–4(f). As we can see, the spectral responses of the actual mesh deviate significantly from those of the ideal mesh, indicating that configuring the mesh based on an ideal assumption would lead the actual defective mesh to deviate from the targeted functionality. Also, the spectral responses of the characterized mesh align with those of the actual mesh, validating the effectiveness of our characterization method in accurately predicting the actual mesh behavior. Then, we configured the filters using voltages chosen based on the characterized ${\widehat{\mathit{C}}}_{\mathit{p}}$, the normalized spectral responses of the actual and the characterized mesh are plotted in Figs. 4(g)–4(i). As we can see, they are in perfect alignment, and both have achieved the intended functionality, highlighting that our characterization method can ensure configurations suitable for the actual defective mesh.

We also demonstrated the implementation of IIR filter applications, including an optical ring resonator (ORR), a triple ORR coupled-resonator waveguide (CROW) filter, and a double ORR ring-loaded MZI. Similarly, we observed a phenomenon comparable to that seen in the FIR filter configurations (see Sec. S9 in the Supplementary Material for more details). The successful implementation of the FIR and IIR filters proves the effectiveness of our method in configuring applications on meshes with fabrication errors.

Our characterization method combines the optimization method with a step-by-step parameter-space-reduction technique, addressing the challenges in characterizing recirculating waveguide meshes. Under the condition of ${\sigma }_{\mathrm{BS}}=2.5\%$, our method ensures characterizing $K_{\mathrm{BS}}$ of the BSs with an error less than 1.34% in 95% of the cases, characterizing $d{\vartheta }_u$ with an error smaller than $0.0026\pi$ in 95% of the cases, and predicting the transmission matrix of the mesh with an average RMSE of 0.35 dB. We also analyzed the stability and robustness of the proposed characterization method under various scenarios, considering different $K_{\mathrm{BS}}$ variances, inaccuracies in measurements of the mesh, and inaccurate TBU IL characterizations. It has been demonstrated that our characterization method is very robust, exhibiting an average RMSE of 0.8 dB under the circumstance of ${\sigma }_{\mathrm{BS}}=2.5\%$, ${\sigma }_{\mathit{T}}=5\%$, and ${\mu }_{\mathrm{IL},e}=0.2\mathrm{dB}$. We also apply our method to implementing various FIR and IIR applications, confirming the effectiveness of our method in configuring applications on meshes with fabrication errors. Our method can greatly broaden the range of imperfection parameters that can be characterized, making it sufficient for use in simulation methods and analytical gradient calculation methods, thus providing the last crucial element needed to achieve a much faster off-chip configuration. It can also be used to furnish initial voltage settings before conducting on-chip configuration.

Please refer to the Supplementary Material for more discussion on the modeling of imperfect recirculating waveguide meshes, the detailed principles of the characterization method, the robustness analysis of the method, and its practical applications.