Jiahao Dong, Liang Xu, Yiqi Fang, Hongcheng Ni, Feng He, Songlin Zhuang, Yi Liu, "Scheme for generation of spatiotemporal optical vortex attosecond pulse trains," Photonics Res. 12, 2409 (2024)
Search by keywords or author
- Photonics Research
- Vol. 12, Issue 10, 2409 (2024)
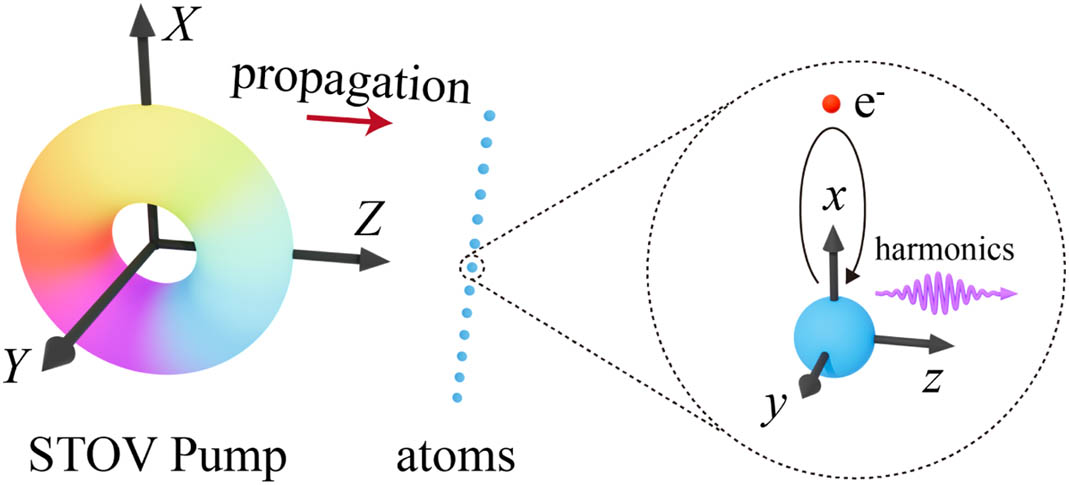
Fig. 1. Sketch of the discrete spatial electric dipole approximation. A STOV pumping pulse irradiates a blob of hydrogen atoms, and atoms at different X ( X , Y , Z ) ( x , y , z ) ( X , Y = 0 , Z = 0 )

Fig. 2. (1st column) Spatial-resolved HHG spectra driven by STOV pulses and retrieved spatiotemporal (2nd column) intensity and (3rd column) phase distributions of the 35th harmonic. (a) Only FW field with λ FW = 1600 nm ϕ = 0 ϕ = 1.1 π I FW = 1 × 10 14 W / cm 2 I TH = 9 × 10 12 W / cm 2
Fig. 3. Diagrams of the time-frequency analyses of the HHG emission (X = 0 2 (a1)–2 (c1), respectively.
Fig. 4. Classical electron trajectories driven by laser fields at X = 0 2 (a1)–2 (c1), respectively. The blue, green, yellow, and red curves represent an electron trajectory with one, two, three, and four or more returns, respectively. The line thickness represents the relative magnitude of the ionization rate after logarithmic treatment. Note that only trajectories where electrons are able to return and the ionization rate is greater than 10% of the maximum ionization rate are shown, and about half of the laser field is shown by the black dashed line.
Fig. 5. Retrieved spatiotemporal intensity distributions of APT in (a), (b), and (c) correspond to Figs. 2 (a1), 2 (b1), and 2 (c1), respectively. (d) Temporal intensity profiles of a single attosecond pulse sampled from the black rectangle in (c). The red dotted curve represents a Gaussian fitting with an FWHM of 613 as.
Fig. 6. Spatially-resolved 35th harmonic spectra, I TH = 9 × 10 12 W / cm 2 I TH = 4.9 × 10 13 W / cm 2 I TH / I FW I FW = 1 × 10 14 W / cm 2 X = 0
Fig. 7. Distribution of cos ( 2 ω t − 2 φ f ) X – t φ f

Set citation alerts for the article
Please enter your email address



