Femtosecond laser systems are widely used in biomedical science, high-precision material processing, and ultrafast nonlinear optics, by virtue of their advantages of high peak power, low thermal impact, and high precision^[1-4]. Compared to solid-state lasers, fiber lasers not only deliver femtosecond pulses with repetition rates ranging from kilohertz to megahertz, but also hold the advantages of high beam quality, high conversion efficiency, convenient thermal management, and compact structure. However, the pulse quality degrades with the power scaling due to higher-order nonlinearities during the power amplification^[5]. Chirped-pulse amplification (CPA) is considered as one of the most effective solutions to improve the pulse quality of high-power amplification systems^[6]. Generally, the chirped pulse output from the seed laser is temporally stretched to a nanosecond duration and amplified in a large mode area (LMA) fiber or rod-type photonic crystal fiber^[7,8]. Highly chirped pulses accumulate less nonlinearity in the amplification process, making it possible to compress the duration of the amplified pulse close to the transform limit (TL). Another solution is nonlinear amplification based on pre-chirp management, spectral amplitude shaping, or gain management^[9-11]. Although the pulse duration can be reduced to sub-100-fs because of the spectral broadening, the corresponding pulse energy is limited to several microjoules to tens of microjoules.

Regardless of which amplification structure is used, the pulse-duration stability of high-energy laser systems is crucial for both industrial applications and fundamental researches^[12-14]. However, due to ambient thermal and mechanical vibrations, the pulses output from the laser system manifest the instability of pulse durations, which is unfavorable for applications demanding high pulse-duration stability. Small adjustments to pulse stretchers or compressors by trained researchers to rebalance system dispersion are a straightforward correction^[15,16]; however, it is clearly not a paradigm that can be transferred to industrial manufacturing scenarios. Passive controls such as sealing treatment and thermal management of the laser system as well as active stabilization of the amplifier pump current are not immune to the effects of the external environment on pulse duration.

It is possible to achieve automatic pulse optimization by using a pulse shaper^[17]. With the support of the evolutionary algorithm, hundreds of different phases introduced by a spatial light modulator (SLM) make the pulse duration converge toward TL^[18]. With the development of ultrashort pulse characterization, the reconstruction of spectral phases can be achieved through techniques such as multiphoton intra-pulse interference phase scan (MIIPS)^[19], spectral phase interferometry for direct electric-field reconstruction (SPIDER)^[20], and frequency-resolved optical gating (FROG)^[21]. Among these techniques, MIIPS compensates spectral phases through an SLM to obtain TL pulses, which is also used as a high-performance pulse compressor. Recently, given the predictable changes in the second harmonic (SH) spectrum that depend on spectral phase, a real-time MIIPS has been used to achieve automatic pulse optimization^[22]. However, limited by the response speed of the SLM and phase iterations, a single-shot pulse optimization still took about 100 ms. For many cases, it is straightforward and efficient to optimize the pulse-duration drift by feeding back the SH intensity to the grating compressor^[23]. For example, despite periodic fluctuations in ambient temperature ranging from 23.2°C to 29.0°C, combining the fast pulse-duration detection based on two-photon absorption (TPA) and embedded software to adjust the system dispersion, the sub-picosecond pulse remains relatively stable for a long time^[24]. The above experiment only described a method and the resultant performance data for the pulse-duration stabilization, while avoiding mentioning the algorithm of the feedback control. Until now, the design of the field pulse-duration stabilization algorithm for multiple scenarios is still an open issue.

In this paper, we propose a field programmable gate array (FPGA)-based PDFC applied in an all-fiber femtosecond CPA system. The SH signal generated from a beta-barium borate (BBO) crystal is extracted by the FPGA, whose PD response can represent the actual pulse duration. A stepper motor controlled by the FPGA drives the grating to compensate artificially introduced fluctuations of pulse duration. Given the hardware feedback loop, a hybrid control algorithm consisting of the improved stochastic hill-climbing search (HCS) and incremental proportional-integral (PI) controller is dedicatedly designed to realize the field stabilization of pulse duration.

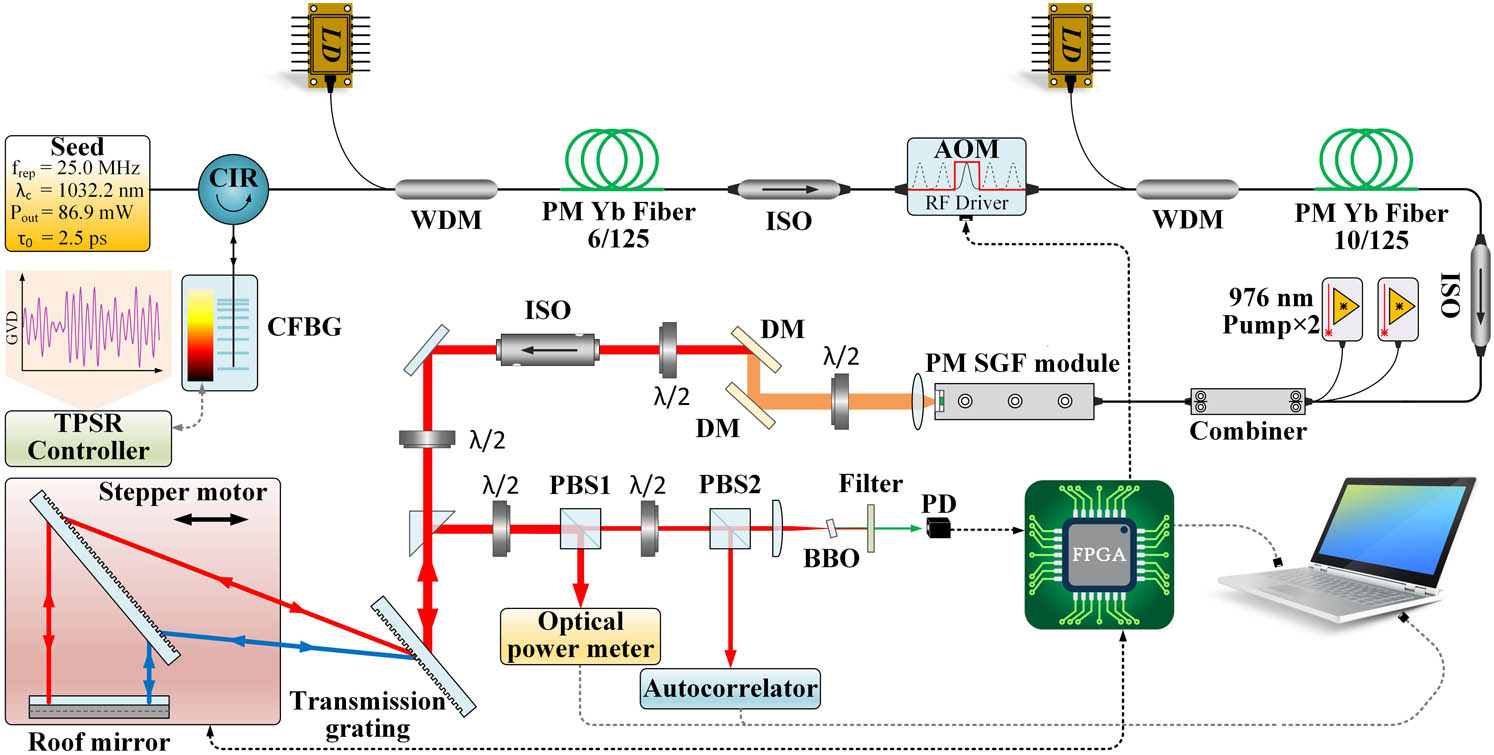
The schematic diagram of the all-fiber femtosecond CPA system with a PDFC is shown in Fig. 1, which consists of a seed laser, a pulse stretcher, a pulse picker, three stages of all-fiber amplifiers, a transmission grating-pair pulse compressor, and an FPGA-based feedback loop.

The seed laser is a Yb-doped mode-locked fiber laser (NPI Lasers, Blade-seed fs), which generates the pulses with a repetition rate of $\sim 25\mathrm{MHz}$. The output pulses are coupled into a fiber circulator and temporally stretched by a chirped fiber Bragg grating (CFBG, Teraxion, TPSR-1030T-25F) tunable pulse stretcher. The reflective CFBG stretcher can provide a group velocity dispersion (GVD) and a third-order dispersion (TOD) of $19.457{\mathrm{ps}}^2$ and $-0.172{\mathrm{ps}}^3$, respectively. Afterwards, a single-mode pre-amplifier is used to compensate for the following power attenuation from the insertion loss of the acoustic optical modulator (AOM) and pulse picking ratio. The gain medium is a 1.5-m highly doped Yb-fiber (Nufern, PM-YSF-HI) with a 6-µm core diameter, which is pumped by a 976-nm single-mode laser diode (LD) via a wavelength division multiplexer (WDM). In order to reduce the repetition rate from 25 MHz to 1 MHz, a fiber-coupled AOM is employed, which is driven by a 200-MHz radio frequency (RF) driver. The input signal and its time delay of the RF driver are generated by the FPGA, which is triggered by the synchronous output from the seed laser. Then, the average power is scaled up by a boost-amplifier. A 1.5-m Yb-doped active fiber (Nufern, PLMA-YSF-10/125-M) with a 10-µm core diameter is employed to mitigate the nonlinear accumulation. An isolator (ISO) is inserted behind the active fiber to prevent the irreversible optical damage from the backward light.

The boosted pulses are coupled into the main-amplifier via a $(2+1)\times 1$ fiber combiner. A commercial ultra-highly Yb-doped LMA polarization-maintaining (PM) silicate glass fiber module (AdValue Photonics, AP-AMP-MOD-1030-G2) is forward-pumped by a 60-W multimode laser diode. The length of the gain fiber is only 20 cm, while the gain exceeds 23 dB. The mode field diameter is 40 µm. The output end of the gain fiber is spliced by an angle polished endcap to avoid the back-reflected light and its re-amplification^[25]. The main-amplifier module and fiber combiner are water cooled at 25°C. The output laser pulses from the main-amplifier are spatially collimated by an aspheric mirror and subsequently de-chirped by a double-pass compressor, which consists of a pair of 1600 lines/mm transmission gratings (LightSmyth, T-1600-1030s) and a roof mirror. The laser pulses are incident to the surface of the transmission grating at a Littrow angle of 55.5°. Finally, the laser pulse is output from the reflection port of the polarizing beam splitter (PBS) 1 and received by an optical power meter for monitoring its average power.

The pulse-duration feedback relies on a photodetector (PD), an FPGA with an analog-to-digital converter (ADC) and a digital-to-analog converter (DAC), and a stepper motor. The SH pulse generated from a 0.2-mm long and $4\mathrm{mm}\times 4\mathrm{mm}$ aperture BBO crystal ($\theta =23.4°$, type 1) is detected by the PD. The pulse signal is sampled by the ADC after passing through a low-pass filter with a 10-kHz cutoff frequency. The ADC reading is an equivalent integral value of the pulse signal, representing the average power of the SH pulse. In the following, we refer to the ADC reading of the SH pulse as “PD response”. On the other hand, one transmission grating is installed on the stepper motor for coarse/fine adjustment of the compression distance. The absolute position of the stepper motor is controlled by applying a voltage provided by the DAC to its driver. The movement of the stepper motor depends on the instructions sent by an algorithmic framework according to the PD response. The control algorithm will be illustrated in Section 3.

The optical spectra are monitored by an optical spectrum analyzer (OSA, Yokogawa AQ6370D) with a 0.02-nm resolution. The compressed pulses are measured by an autocorrelator (APE Pulse Check).

After power-on, the seed laser immediately operates in a stable mode-locked state and delivers the pulses with an 86.9-mW average output power. As shown in Fig. 2(a), the spectral 3-dB bandwidth of the pulse is 14.7 nm with a center wavelength at 1032.2 nm. The corresponding output pulse duration is 2.5 ps according to the autocorrelation trace depicted in Fig. 2(b). Afterwards, to reduce the peak power, the pulses are temporally stretched to $\sim 550\mathrm{ps}$ by the CFBG stretcher. After passing through the sandwich structure of two pre-amplifier stages and AOM-based pulse picker, the average power is scaled up to 140 mW and the repetition rate is reduced to 1 MHz. Then, the main-amplifier scales up the average power to 21.8 W. Figures 2(c) and 2(d) depict output characteristics of the amplified pulses. The spectral 3-dB bandwidth is reduced to 7.4 nm compared with that of the seed laser, owing to the gain narrowing effect of three stages of all-fiber amplifiers^[5]. By carefully adjusting the vertical distance of the transmission grating pairs and finely tunning the dispersion coefficient of CFBG, the pulses can be de-chirped to 236 fs, close to TL pulse duration of 211 fs shown by the red dashed curve in Fig. 2(d). However, obvious pedestal of the compressed pulse indicates that nonlinear chirp caused by self-phase modulation during high-power amplification cannot be compensated. The average power and the single pulse energy of the output from the compressor are 15.9 W and 15.9 µJ, respectively, corresponding to a compression efficiency of 73%.

In order to implement the field stabilization of pulse duration, measurement methods to quickly monitor and characterize the pulse duration are indispensable. However, a single measurement time of pulse duration takes approximatively 0.5 s based on the mechanically scanned autocorrelation trace, severely restricting the speed of the feedback control. For that, a BBO crystal is employed to generate the SH pulse, of which the PD response is dependent on the incident pulse duration. Specifically, the shorter pulse duration corresponds to the higher excitation efficiency of the SH signal because of the TPA effect^[26]. As shown in Fig. 3, when the absolute position of the stepper motor is scanned from 7.5 mm to 10.5 mm with a step length of 20 µm, the pulse duration is inversely proportional to the PD response. During the scanning process, the reading of PD response for each motor position is triggered by the single autocorrelation trace measurement. Actually, the reading speed of PD response in the feedback control is $\sim 5\mathrm{ms}$, which is 100 times faster than the time cost of a single autocorrelation trace measurement. Without loss of generality, we record 10 sets of scanning results and calculate the average value as the final result, confirming the consistency of the pulse duration and the corresponding PD response.

Figure 4 shows the performance of the free-running CPA system within a 60-min stability test. We calculate the peak-to-peak fluctuation, standard deviation (STD), and root-mean-square error (RMSE) to evaluate the system stability. The RMSE of the output average power within 60 min is 0.094%, as shown in Fig. 4(a). On this premise, the PD response monitored after the BBO crystal can uniquely represent the variation of pulse duration. The RMSEs of the PD response and pulse duration are both around 1%, proving the excellent stability of the CPA system, as shown in Figs. 4(b) and 4(c). The actual fluctuation of pulse duration might be lower than 8.7%, because part of pulse-duration fluctuation may originate from the measurement error of the autocorrelator caused by the beam pointing. In our experiments, all the tests are performed under the same conditions without any active compensation for beam pointing.

In the following experiments, a random amplitude perturbance is applied to the GVD provided by the CFBG to introduce temperature-induced pulse-duration fluctuations. Therefore, we can verify the feasibility of the algorithm by eliminating the artificially introduced fluctuations of pulse duration. The control algorithm of pulse-duration field stabilization, refers to a hybrid algorithm consisting of improved stochastic HCS and incremental PI controller. The function of improved stochastic HCS is to calibrate the PD response corresponding to the minimum pulse duration and to set the target pulse duration. Subsequently, the incremental PI controller stabilizes the pulse duration around the pre-set target value.

The HCS is a local search algorithm that aims at finding a local maximum of the objective function by making incremental changes and selecting the update or original solution that leads to the most improvement^[27]. Therefore, the HCS is suitable for the objective function with a single extremum shown in Fig. 3. In the experiment, we used an improved stochastic HCS to optimize the searching process, by which the optimal motor position corresponding to the minimum pulse duration can be searched in every single running.

Figure 5(a) shows the framework of improved stochastic HCS with a single input and a single output. In order to prevent the error that the stepper motor receives a negative-stroke instruction at the zero-position, we set the initial motor position $x$ at 2 mm and query the ADC reading at the current position. The incremental change $\mathrm{\Delta }x$ is randomly selected from $U(-{\mathrm{\Delta }}_{\max },{\mathrm{\Delta }}_{\max })$, and ${\mathrm{\Delta }}_{\max }$ determines the boundary of the uniform distribution. We query the ADC reading at the new position $\widehat{x}=x+\mathrm{\Delta }x$ and compare the size of $I_{\widehat{x}}$ at the new position and $I_x$ at the original position. If $I_{\widehat{x}}>I_x$, update $x$ by $\widehat{x}$ to approach the maximum value. Conversely, if $I_{\widehat{x}}<I_x$, select a new $\mathrm{\Delta }x$ from $U(-{\mathrm{\Delta }}_{\max },{\mathrm{\Delta }}_{\max })$ and repeat the process above. So far, the algorithm completely runs as a standard stochastic HCS. However, the initial confidence interval of $\mathrm{\Delta }x$ is too large, making it difficult to search for a precise maximum value. Thus, if the $x$ is not updated within consecutive 10 stochastic HCSs ($N>10$), the confidence interval for $\mathrm{\Delta }x$ will be reduced by a factor of $m$, here set to 1.6. While the motor position is not updated for a long time ($M>60$), the algorithm is finally quitted and output $I_x$.

The searching process of the minimum pulse duration is recorded in Figs. 5(b)–5(d). After the algorithm starts, the objective function (PD response) rapidly approaches the maximum value, as depicted in Fig. 5(c). If $x$ is not updated, the stepper motor will return to $x$-position, otherwise move to the updated $\widehat{x}$-position. The range of the variation of PD response gradually becomes smaller for the continuous shrinking of the confidence interval of $\mathrm{\Delta }x$. Finally, the PD response converges to the maximum value after multiple attempts. During this process, the position of the stepper motor fluctuates around the optimal position corresponding to the maximum PD response, as depicted in Fig. 5(b). The variation of pulse duration exhibits a smooth decline and converges to the minimum pulse duration due to the low sampling rate, as depicted in Fig. 5(d). It is worth noting that the random amplitude perturbance of the pulse duration has been applied to the CFBG before the start of improved stochastic HCS, indicating that the perturbation of grating position provided by the algorithm is not affected by the modulated pulse duration.

After calibrating the maximum PD response corresponding to the minimum pulse duration, we set the target PD response according to $$\widehat{I}=I_x-I_0,$$(1)where different $I_0$ determine different target pulse durations. Then, the incremental PI controller stabilizes the pulse duration to approach the pre-set $\widehat{I}$, which is attributed to the fact that the PI control is more suitable for use in a monotonic interval.

The PI controller, as a popular industrial feedback loop in automatic control systems, consists of a proportional controller and an integral controller^[28]. In general, the output of the proportional controller is proportional to the error, and the integral controller integrates the error to eliminate the static error of the system. Here, we used the incremental PI controller to reduce the error caused by the sampling of the ADC^[29,30]. In the experiment, we calculate the error according to $$e(k)=\widehat{I}-I_k,$$(2)where $I_k$ represents the $k$-th measurement value of PD response. The output of incremental PI controller is a relative movement $\mathrm{\Delta }X$ of the stepper motor (differs from $\mathrm{\Delta }x$ in improved stochastic HCS algorithm), which is calculated by $$\mathrm{\Delta }X=(K_p·\mathrm{\Delta }e(k)+K_i·e(k))/\alpha ,$$(3)where $\mathrm{\Delta }e(k)=e(k)-e(k-1)$, which characterizes the difference between $k$-th and $(k-1)$-th errors to reduce the sampling error, $K_p$ and $K_i$ are the gains of the corresponding terms, set to 0.35 and 0.15, respectively, and $\alpha$ is used to modify the step length of the stepper motor, set as 1/5000 here.

Figures 6(a)–6(c) show a typical initial stage of the incremental PI controller. The stepper motor moves smoothly to the position corresponding to the target value of the PD response, according to the output $\mathrm{\Delta }X$ of incremental PI controller. In order to verify the performance of the PDFC algorithm, the pulse-duration fluctuation introduced by the CFBG is much larger than that in the actual CPA system. Figures 6(d) and 6(e) show the random amplitude perturbance of GVD and the corresponding variation of pulse duration without the control algorithm, respectively. When entering the stable stage, the fluctuations of pulse duration are obviously well suppressed compared with the case without the algorithm, as shown in Fig. 6(f). The peak-to-peak fluctuation of pulse duration is reduced from 37% to 6.5%, namely the stability of pulse duration is improved $\sim 5.7$ times. Simultaneously, the trajectory of the stepper motor movement is highly consistent with the change of the pulse duration without the incremental PI control, indicating the field compensation ability of the feedback control.

In order to exhibit the performance robustness of the PDFC, a 60-min pulse-duration stability test and robust switching between different pulse durations are depicted in Fig. 7. The random amplitude perturbance of GVD in Fig. 7(a) is controlled by the tunable CFBG pulse stretcher. Specifically, fine temperature control changes the dispersion coefficient provided by the CFBG, manifested as a perturbation of the compression distance for a specific pulse duration. Algorithm-dependent field modification of the compression distance is achieved by high-speed control of the stepper motor to cope with temperature-induced pulse-duration fluctuations. As shown in Fig. 7(b), the pulse duration converges and is stabilized around 258 fs. Because of the need for incremental PI controller to operate within a monotonic interval, the stabilized pulse duration is set at a position slightly deviated from the optimum value. The peak-to-peak fluctuation of pulse duration is reduced to 7.0% and the RMSE is only 0.97%, comparable to the free-running case in Fig. 4(c), indicating the complete suppression of artificially introduced fluctuations and proving the excellent performance of PDFC algorithm.

In addition, the robust switching between different pulse durations can also be achieved by modifying the target value. Figure 7(c) demonstrates the switching between different pulse durations by changing pre-set position of the stepper motor, which is commonly used in industrial femtosecond lasers. In the experiment, the support of the control algorithm not only realizes the switching function, but also stabilizes the pulse duration around the pre-set value, as shown in Fig. 7(d). The fluctuations without algorithmic control are represented in the form of “error bars”, illustrating the obvious suppression of temperature-induced pulse-duration fluctuations by the BBO-based feedback control. The robust switching between different pulse durations may offer new perspective on tunable high-power femtosecond lasers for future applications in high-precision machining and laser medical treatment^[31].

It is worth mentioning that the BBO-based feedback control must be on the premise of the stable output average power, so that the intensity of SH signal uniquely reflects the variances of pulse duration. The average power stability could be improved by controlling the pump current of fiber amplifiers and/or embedding a feedback loop of the RF power injected into an output AOM^[32]. As for field stabilization of the shorter pulse duration, especially sub-100 fs pulses, a shorter BBO crystal is indispensable, otherwise the walk-off of the group velocity between the fundamental-frequency pulse and SH pulse in the BBO crystal will cause a mismatch between the PD response and the pulse duration. On the other hand, considering that sub-100 fs pulses are more sensitive to the compression distance, a stepper motor with a shorter step length or a piezo actuator is also needed for more precise adjustments^[31]. Furthermore, high-power femtosecond lasers have versatile configurations according to different requirements such as ultrashort pulse durations, high pulse energies, and low repetition rates. Without loss of generality, the field stabilization of pulse duration is not only suitable for CPA systems, but also can be widely used in other femtosecond pulse amplifiers.

An automatic PDFC employed in a femtosecond CPA system is realized through the hardware foundation of a BBO crystal, an FPGA, and a stepper motor combined with the algorithmic framework of improved stochastic HCS and incremental PI controller. Specifically, according to the PD response of SH signal generated from the BBO crystal, the changes in the vertical distance of the grating-pair compressor controlled by the stepper motor can effectively compensate for the fluctuations of pulse duration. A random amplitude perturbance of pulse duration is introduced to evaluate the performance of the control algorithm. On this premise, structured in the order of the improved stochastic HCS and incremental PI controller, the control algorithm firstly finds the PD response corresponding to the minimum pulse duration, sets the target value, and then stabilizes the pulse duration around the pre-set value. The peak-to-peak fluctuation of pulse duration is reduced from 37% to 6.5% with the PDFC, indicating the excellent compensation ability of the algorithm for temperature-induced pulse-duration fluctuations. The 60-min stability test of a specific pulse duration and robust switching between different pulse durations demonstrate that PDFC has the ability to be applied in multiple scenarios. We believe this feedback control method could offer a novel insight into active control of output characteristics of high-power femtosecond lasers and have extensive prospects in diverse applications.