Multi-wavelength laser sources have attracted wide attention in various fields, such as optical communication, satellite laser ranging, material application, lidar, digital imaging, biomedicine, terahertz (THz), sensing, and so on^[1-3]. Stimulated Raman scattering (SRS) is an effective method to realize a multi-wavelength output, which can work in a wide range of durations, from continuous wave (CW) to femtosecond pulse, and has been applied in a number of fields^[4-6]. W.S. Yoo et al.^[7] demonstrated that multi-wavelength Raman spectroscopy has the capability of measuring advanced and sophisticated device structures. J.F. Hu et al.^[8] applied the picosecond multi-wavelength Raman laser to satellite laser ranging system, and D. Althausen et al.^[9] reported that the resolution of the multi-wavelength laser source was superior to the monochromatic laser in ranging. Compared with the nanosecond laser source, many more reports have confirmed that the picosecond laser source could present much more desirable performances in some applications^[10-12], such as a higher precision and greater resolution. However, as the pump source for SRS, the picosecond laser has a lower Raman gain and Raman efficiency compared with the nanosecond laser, in addition, the Raman gain factor of a long-wavelength pump source is also lower than that of the short-wavelength pump source^[13]. A kind of synchronously external resonator pump setup was widely employed to improve the SRS gain and conversion efficiency for the infrared picosecond pump configuration. In 2019, M. Frank et al.^[14] introduced a picosecond synchronously pump external Raman laser that achieved three infrared lines, with an overall Stokes output pulse energy of about 5 nJ. The synchronous external cavity was suitable for the case where the repetition frequency is at least several tens of MHz with output energy of an nJ-level. Therefore, the cavity length is generally designed to be 1−2 m and sensitive to detuning. However, for a 1 kHz picosecond pump source, the external cavity length of the synchronously pump scheme needs to be designed to 1.5 × 10⁵ m, which is difficult to achieve. Compared with the synchronously pump scheme, the single-pass pump structure without a resonator works more stably and is not restricted by the repetition frequency, which still attracts research interest and is popularly employed in some industrial and commercial areas. In order to improve the Raman gain of picosecond single-pass configuration and avoid the operating instability induced by the long cavity, we introduced a multi-pulse burst pumping scheme for the SRS process of the 1 kHz picosecond pump source.

Multi-pulse pump scheme used in Raman system is an important technique to study the properties of Raman media and improve the performance of SRS. In 2010, K.C. Lee and B.J. Sussman et al.^[15] used the method of transient coherent ultrafast phonon spectroscopy (TCUPS) to measure the dephasing lifetime of the diamond, which can achieve a higher relative resolution than the traditional method. In the same year, it was also P.J. Bustard and B.J. Sussman et al. that adopted a multi-pulse scheme to achieve the amplification of excited molecular rotational coherence with a stable phase in hydrogen gas^[16]. In addition, the multi-pulse bursts are usually employed in the transient Raman regime to improve the Raman gain. In 1990, L.R. Marshall and J.A. Piper^[17] adopted dual-pulse pump Pb vapor to improve the Raman conversion efficiency from 15% to 35%, where the pulse duration was 6 ns and pulse interval was set to 15 ns. Unlike the gas Raman media, crystalline Raman media usually have a shorter dephasing time. In the case of picosecond pumping, the pulse duration is usually longer than the dephasing time of the Raman crystal, which approximates the steady Raman regime. Different from the transient Raman regime where the buildup effect is related to the dephasing time of the Raman active molecule, while for the steady Raman regime, we found that the enhancement effect is related to the oscillation duration of the Raman active molecule. In 2016, X. Gao^[18] introduced a multi-pulse burst pumping regime to reduce the picosecond SRS threshold in the visible waveband, which utilized the cumulative effect of the Raman active molecule to the impulse response. Following this research, we analyzed in detail the effects of the multi-pulse burst on the Raman process in the steady Raman regime, which was based on the picosecond laser source and the solid Raman medium of a KGd(WO₄)₂ (KGW) crystal (dephasing time of 1.7 ps). On the basis of the vibration theory, we developed a mathematical model to simulate the effect of the multi-pulse burst pumping regime on the vibrational mode of the Raman active molecule, which implied that the multi-pulse burst excitation can effectively improve the Raman gain. Next, we compared the achievements of the single, dual, and three 1 064 nm picosecond pulse burst pumped KGW crystal schemes. The experimental results indicate that the three-pulse burst pumping regime shows the best performance - with the Raman gain improving more than two times, the SRS threshold reducing more than 50%, and the Raman conversion efficiency increasing more than 16% (768 cm^–1) and 22% (901 cm^–1).

To obtain a picosecond infrared Raman laser with a high energy and high-order Stokes infrared radiation, in this work, we designed a 1 kHz infrared picosecond multi-pulse burst Raman laser, which adopted the method of multi-pulse burst pumping. Based on the three sub-pulses burst regime, the Raman laser obtained a maximum overall Stokes average power of 1.39 W for the 768 cm⁻¹ vibrational mode, and 1.38 W for the 901 cm⁻¹ vibrational mode, which raised the output pulse envelope energy of a picosecond pump KGW Raman laser up to a mJ level. Meanwhile, up to eight infrared Raman lines were achieved in total.

The excitation vibration of the Raman active molecule was assumed as a stimulated simple harmonic oscillator when excited by the injected light field^[19], which can be described as follows:

$ \frac{{{{\rm{d}}^2}q}}{{{\rm{d}}{t^2}}} + 2\gamma \frac{{{\rm{d}}q}}{{{\rm{d}}t}} + \omega _n^2q = \frac{{F\left( t \right)}}{m} $  (1)

where ω_n is the natural vibration frequency of the harmonic oscillator, m is the reduced nuclear mass, and γ is the damping constant, as follows γ~exp[-(t_c-t_w)/(t_a·T₂)], and in which the parameters t_c, t_w, t_a, and T₂ represent the interval of adjacent pulse within the burst, pulse duration, molecule oscillation duration, and dephasing time, respectively. q(t) represents the deviation of the internuclear distance from its equilibrium value q₀, and F(t) denotes the force that acts on the molecule vibrational mode. The response of the molecule vibrational mode to a unit impulse excitation started at t=τ can be expressed as follows^[20]:

$ h\left( {t - \tau } \right) = \frac{1}{{m{\omega _d}}}{e^{ - \zeta \left( {{\omega _L} - {\omega _S}} \right)\left( {t - \tau } \right)}}\sin {\omega _d}\left( {t - \tau } \right){\rm{ }} $  (2)

where ω_L and ω_S are the pump field frequency and Stokes field frequency, respectively. ζ and ω_d denote the damping ratio and the frequency of damped oscillator respectively, and given by the following:

$ $$\begin{array}{l}\zeta ={\displaystyle \frac{\gamma }{{\omega }_n}}\\ {\omega }_d=\sqrt{1-{\zeta }^2}{\omega }_n\end{array}$$ $  (3)

Furthermore, the response of the vibrational mode to the driven force F(t) of arbitrary excitation can be represented by the following integral:

$ q\left( t \right) = \int_0^t {F\left( \tau \right)} h\left( {t - \tau } \right){\rm{d}}\tau $  (4)

Substituting Eq.(2) into the Eq.(4), we arrive at the following equation:

$ q\left( t \right) = \frac{{\rm{1}}}{{m{\omega _d}}}\int_0^t {F\left( \tau \right)} {e^{ - \zeta \left( {{\omega _L} - {\omega _S}} \right)\left( {t - \tau } \right)}}\sin {\omega _d}\left( {t - \tau } \right)d\tau $  (5)

Equation (5) is called the Duhamel integral, which represents the molecule oscillation driven by the applied excitation force. Assuming that the optical excitation obeys a Gaussian type, the applied optical excitation signal of a multi-pulse burst can be described as follows:

$ I\left( t \right) = \frac{A}{{\sqrt {2\pi } {t_p}}}\sum\limits_{k = 1}^n {{e^{ - \frac{{{{\left( {t - k \cdot {t_0}} \right)}^2}}}{{2t_p^2}}}}} \cdot \frac{1}{{\pi {r^2}}} $  (6)

where t₀ is the peak moment of a sub-pulse excitation signal, t_p represents the temporal duration of a sub-pulse, n is the number of sub-pulses contained in a pulse-burst group, A denotes the optical amplitude, and r is the spot radius. The driven force exerted on the molecular oscillation by the applied optical field can be given by the following^[19]:

$ F\left( t \right) = \frac{{{\varepsilon _0}}}{2}{\left( {\frac{{{\rm{d}}\alpha }}{{{\rm{d}}q}}} \right)_0}\left\langle {{E^2}\left( t \right)} \right\rangle $  (7)

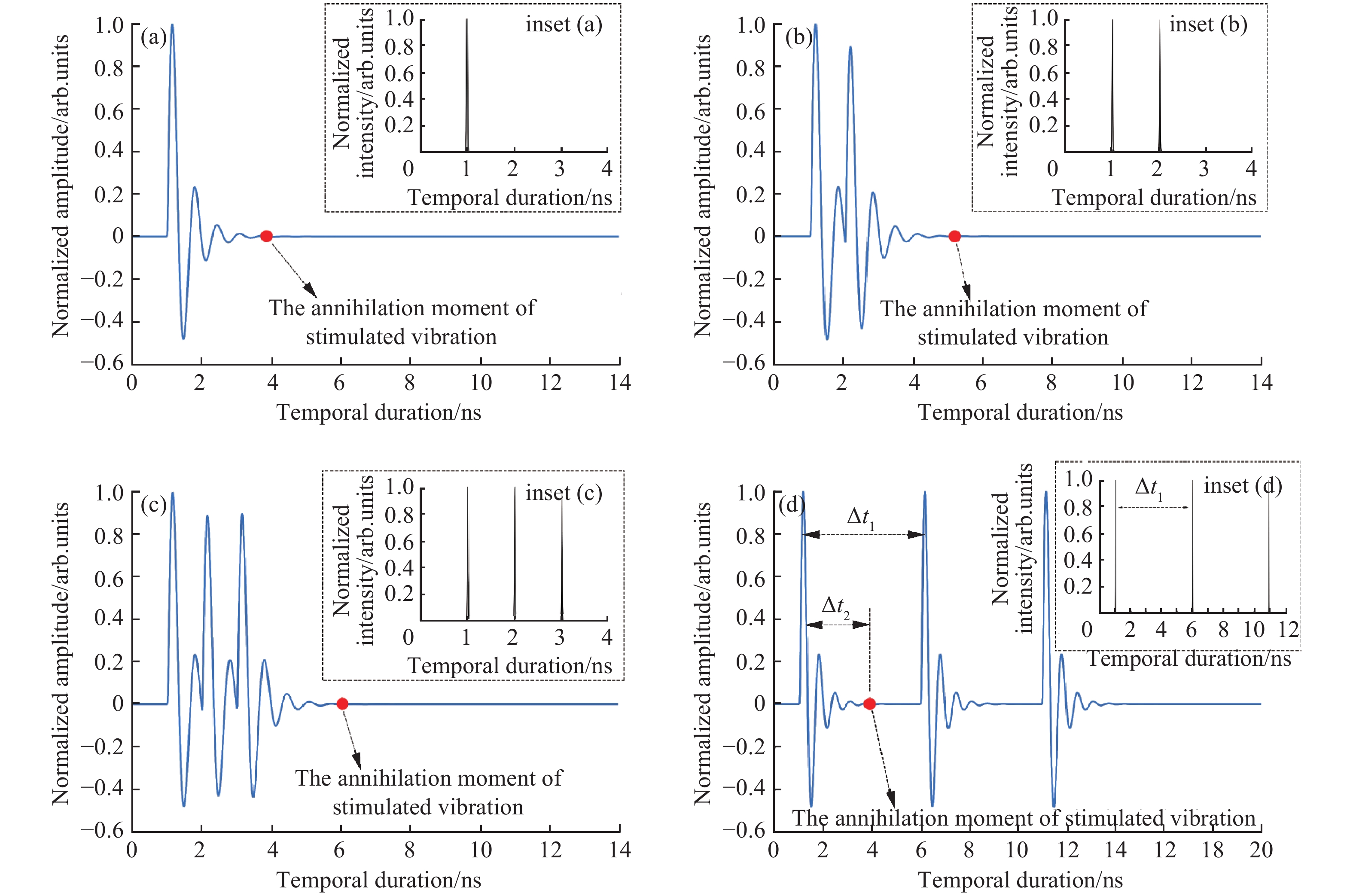
in which ε₀ is the permittivity of free space, α is the optical polarizability of the molecule, E(t) is the applied optical field, and the angular brackets denote a time average over an optical period. Taking the KGW crystal as an example, the response of the molecule vibrational mode to the multi-pulse burst excitation regime can be simulated by inserting Eqs (6) and (7) into the Duhamel integral, and the normalized analysis results are shown in Fig.1, in which the temporal duration of a sub-pulse was 20 ps.

When the optical field interacts with a Raman active molecule, the molecule will initiate a stimulated vibration in response to the optical excitation signal, thereby transferring from the ground state to an excited state. As can be seen from the simulated results of Fig.1, the stimulated vibration is a kind of damped oscillator that lasts for a certain period of time until it is annihilated, and this period is named here as the oscillation duration. In particular, the simulated vibration of the single-pulse excitation signal, shown in Fig.1 (a), is the damped free oscillator, where the duration is referred to as the free oscillation duration and the frequency is referred to as the nature frequency. The impact of the multi-pulse burst excitation signal on the molecule stimulated vibration is mainly reflected in two aspects, as following: on the one hand, the multi-pulse burst excitation regime can drive the response oscillation multiple times to maintain a high amplitude state, which we consider as the oscillation becoming more active; and on the other hand, the multi-pulse burst excitation regime can effectively prolong the oscillation duration. By comparing the figures of 1 (a), 1 (b), and 1 (c), the results imply that the larger the number of sub-pulses in a pulse-burst group becomes, the more significant the effects are. The multi-pulse excitation can enhance the weakened molecular oscillation caused by the damping effect, prompting it to return to the initial oscillation at nature frequency multiple times. The positive influences can enhance the interaction between the optical field and the vibrational mode, which would improve the Raman gain. The Raman gain coefficient can be described as follows^[21]:

$ G = {g_s} \cdot I = {N_g}{\sigma _r}\frac{{\lambda _S^2}}{{h{\omega _L}\delta {{\bar \omega }_{\rm{s}}}}} \cdot \frac{{cn{\varepsilon _0}}}{2}{E^2} $  (8)

in which g_s is the Raman gain factor with the unit of cm/MW, N_g is the number density of molecules, σ_r is the scattering cross section, λ_S is the Stokes wavelength, h is the Planck constant, and $\delta {\bar \omega _{\rm{s}}}$ denotes the average spectral width of the stimulated scattering, n is the refractive index, c and ε₀ are the light speed and dielectric constant in a vacuum, respectively. Taking the 768 cm^–1 vibrational mode of KGW as an example, we simulated the normalized average gain within an optical excitation period of single, dual, and three sub-pulses, respectively, as shown in Fig.2.

It can be seen from Figure 2 that the three sub-pulses excitation scheme shows the largest Raman gain which is approximately three times that of the single pulse. This is the result of multiple oscillations with a high amplitude, which means that the Raman molecule would become more active under multi-pulse excitations and appear as an increase in Raman gain. But, if the temporal distance of the adjacent sub-pulses is longer than the free oscillation duration (Δt₁ > Δ t₂) as shown in Fig.1(d), the multi-pulse burst regime does not have an enhancement effect on the stimulated vibration, which is the same as the excitation influence of the single pulse regime. Therefore, it is important to measure the free oscillation duration in order to set an appropriate temporal interval of adjacent sub-pulses for multi-pulse burst pumping scheme, which will be discussed in the next section.

The measuring setup shown in Figure 3 was developed to determine the free oscillation duration of the KGW active molecule in response to the picosecond Gaussian excitation pulse signal. One 1 064 nm pulse of 20 ps duration was divided into two identical sub-pulses by a 50% beam splitter mirror (BSM). The sub-pulse that transmitted the BSM was called the first sub-pulse, and the sub-pulse reflected by the BSM was called the last sub-pulse. The temporal interval of the two sub-pulses was scaled through a delay optical path. Another BSM was used to combine the two sub-pulses into one optical path. A convex lens, f₁, was used to match the spot of the last sub-pulse to the size of the first sub-pulse spot. Another convex lens, f₂, focused the pump beams to a diameter of 0.7 mm to increase the pump peak power density, and injected it into the KGW crystal. The focal position was set at the center of the KGW crystal. A half-wave-plate (HWP) was adopted to modulate the polarization direction of linear pump beams to match the two Raman modes of KGW crystal. The KGW crystal with a dimension of 7 mm × 7 mm × 30 mm was held in an aluminum heat sink, and was actively water-cooled at a constant temperature of 25 ℃. All of the optical elements in the setup were coated at a pump wavelength of 1 064 nm.

According to the convention, the first Stokes at 1% of the pump spectrum intensity is considered to be the Raman threshold. The Raman spectrum was detected by an infrared fiber optic spectrometer (NIR QUEST (Ocean optics)). The Raman threshold versus the temporal distance of the two sub-pulses is plotted in Fig.4. As the temporal distance increased, the effect of the dual-pulse excitation on the KGW crystal became weak, which was represented by the increase of the Raman threshold. When the temporal distance increased to 3 ns, the Raman threshold no longer grew and tended to be stable, equated to the value of the single pulse pump excitation. With the relation G = 25/(I_thl)^[22] (where I_th is the threshold pump peak intensity and l is the SRS active length of crystal), the gain is inversely proportional to the threshold. It can be analyzed in Fig.4 from two aspects. First, the dual-pulse bursts regime shows the improvement of the Raman gain, and the closer the interval become, the greater the Raman gain improves. Then, the dual-pulse bursts regime no longer improves the Raman gain while the interval is longer than 3 ns, which agrees with the simulations trend shown in Fig.1(d). The experimental results indicated that it would make the enhancement effect that the sub-pulse interval should be less than the free oscillation duration, and the 3 ns was the measured free oscillation duration of this experimental KGW active molecule in response to the picosecond Gaussian pulse signal under these experiment conditions. Different from transient Raman regime where the pulse interval should be shorter than the dephasing time of Raman active molecules, in the steady Raman regime, the pulse interval is mainly related to the measured free oscillation duration which can be affected by the spectral properties, beam quality, temporal structure, and focal position of the fundamental wave^[23-25].

The discussion above implied that the multi-pulse burst pumping regime could present positive effects on the SRS process at the condition of the temporal distance less than 3 ns, and the closer the interval, the better the performance. Therefore, we set the temporal distance to 1 ns in this section, and compared the performance of the single, dual, and three sub-pulses burst pumping regimes from the following three aspects: the Raman gain, the Raman threshold, and the Raman conversion efficiency. The experiment configuration is shown in Fig.5. The 1 064 nm picosecond pulse of 20 ps radiated from a self-produced semiconductor saturable absorber mirror (SESAM) mode-locked master oscillator, which operated at an average power of 500 mW and a repetition frequency of 80 MHz. The three sub-pulses generator realized pulse separation based on an improved Michelson interferometer, which was composed of two BSMs and three 0° high reflection (HR) mirrors. The spatial distance of the adjacent 0° HR mirrors was set to 15 cm, corresponding to the temporal distance of the adjacent sub-pulses of 1 ns. A moveable block was installed in front of each 0° HR mirror to vary the number of sub-pulses from one to three. The separated sub-pulses as seed beams were injected into a self-produced laser amplifier, which was composed of a regenerative amplifier and a power amplifier. Then the seed beams were amplified to a maximum average power of 6 W, and the repetition frequency was reduced to 1 kHz by an electro-optic modulator. Therefore, the amplified multi-pulse burst operated at a repetition frequency of 1 kHz, and was then injected as the pump light into the following Raman generator. To ensure the consistency of the Raman experimental results, the amplifier achieved an equivalent amplitude output within the pulse burst by carefully adjusting the matching of each sub-pulse seed to the laser amplifier. The Raman generator was designed as a single-pass configuration. A half-wave-plate (HWP¹) and a thin film polarizer (TFP) formed a power regulator to scale the pump power from 0 to 6 W. Another HWP² was used to adjust the pump beam polarization direction to match the 768 cm^–1 vibrational mode or the 901 cm^–1 vibrational mode of the KGW crystal. A collimating lens system consisted of a plano-convex lens with R= 150 mm, and a plano-concave lens with R = −75 mm for shaping the pump beams and injecting the pump beams into the KGW crystal in parallel. The b-cut KGW crystal with a size of 7 mm × 7 mm × 30 mm was held in an aluminum heat sink, which was actively water-cooled at a constant temperature of 25 ℃. A long-wavelength pass filter (LPF) with a cutoff wavelength of 1 155 nm was used to screen out the infrared Stokes power and spectra. All the optical mirrors were polished and coated at 1 064 nm. Both of the end faces of the KGW crystal were polished and antireflection coated for the spectrum range of 1.0-2.1 μm (T > 95%). A power meter (Ophir) was used to detect the Raman radiation average power, and two fiber optic spectrometers were employed to detect the Stokes and anti-Stokes lines separately.

We compared the Raman gain, Raman threshold, and Raman conversion efficiency of the single pulse, dual sub-pulses, and three sub-pulses burst pumping regimes, respectively. In the comparative experiment, the pump spot diameter was set to 1.4 mm, and the results are shown in Fig.6. Whether operating in the 768 cm^–1 vibrational mode or in the 901 cm^–1 vibrational mode, the multi-pulse burst pumping regime presented a better SRS output performance than the single pulse pump regime, which was consistent with the theoretical analyses above. The measured Raman gain of the three sub-pulses burst pumping setup for the 768 cm^–1 vibrational mode was about 2.4 times that of the single pulse pump setup, which is shown in Fig.6 (a). The improvement in Raman gain was slightly smaller and less linear than that of mathematical calculations. These differences were mainly due to the incomplete interaction between the pump beams and the Raman crystal, which could be caused by some non-linear factors, including: non-radiative transitions, lattice defects, impurity absorption, etc. In addition, the impure beam polarization induced by the limitations of polarizing elements would also limit the improvement of the gain. For other performances, the Raman threshold was reduced by more than 50% shown in Fig.6 (b), and the Raman conversion efficiency was increased more than 16% (768 cm^–1) and 22% (901 cm^–1) shown in Fig.6 (c). It is noted that the Raman conversion efficiency was measured at the incident pump average power of 3 W for all of the three kinds of pumping regimes, in which the power of 3 W was measured just before the sample of KGW.

As in the comparison above, the three sub-pulses burst pump KGW configuration had the best performance. Therefore, the KGW picosecond infrared Raman laser adopted the three sub-pulses burst pumping regime, and the maximum radiation performance was researched in detail. In the Raman experiment, the pump spot diameter was reduced to 1 mm. Figure 7 plots the Stokes average power and the Stokes conversion efficiency versus the incident pump average power for both the vibrational modes of the KGW crystal.

A maximum Stokes average power of 1.39 W for the 768 cm^–1 vibrational mode and 1.38 W for the 901 cm^–1 vibrational mode was obtained at the maximum incident pump average power of 6 W, corresponding to the pulse-burst energy of 1.39 mJ and 1.38 mJ, respectively. The radiation spectra of the two vibrational modes are shown in Fig.8, which were detected by a fiber optic spectrometer (NIR QUEST (Ocean Optics)). For the 768 cm^–1 vibrational mode, the first-to fourth-order Stokes beams (1 159, 1 272, 1 409, and 1 580 nm) were acquired. For the 901 cm^–1 vibrational mode, the first-to fourth-order Stokes beams (1 177, 1 316, 1 494, and 1 726 nm) were also attained, in addition, the first order anti-Stokes line (971 nm) was detected by this spectrometer. It is noted that the very weak small peaks on the right of each 768 cm^–1 Stokes line are the artifact of the spectrometer. Using a laser beam analyzer (M2-200S (Ophir-Spiricon)), the beam quality factors M² of the fundamental and Stokes wave were 1.38 and 1.27, respectively, which implied the beam cleanup effect of the SRS process.

As can be seen from Fig.7 (b), a roll-over phenomenon was found for the Stokes conversion efficiency, which is reflected in the decrease of the values with the further increase in pump power. In the experiment, the maximum Stokes conversion efficiency of the 768 cm^–1 vibrational mode was 29.6% at the pump average power of 3.6 W, the maximum Stokes conversion efficiency of the 901 cm^–1 vibrational mode was 25.7% at the pump average power of 4.4 W, and the Stokes conversion efficiency tended to decrease with the further increase in pump average power. We considered that this downward trend was due to the thermal effect, which induced a four-wave-mixing (FWM) in the SRS process. Unlike the SRS effect, the FWM effect needs to meet the phase matching conditions, and the Stokes that met the phase matching conditions was converted to the anti-Stokes. This conversion resulted in a decrease in the Stokes conversion efficiency and an increase in the anti-Stokes spectra. At the maximum pump average power of 6 W, we removed the LPF and detected the anti-Stokes lines by another fiber optic spectrometer (USB 2000+ (Ocean Optics)), which is shown in Fig.9. For the 768 cm^–1 vibrational mode, the first-to fourth-order anti-Stokes beams (987, 915, 855, and 802 nm) were obtained. For the 901 cm^–1 vibrational mode, the first-to fourth-order anti-Stokes beams (971, 893, 826, and 769 nm) were also observed. In total, A mJ-level picosecond single pass Raman laser was obtained, which had the ability to radiate up to eight infrared Raman lines for both of the vibrational modes of the KGW crystal. These output properties indicate that the multi-pulse pumping scheme is a worthwhile solution for the design of Raman laser with a high power, high efficiency, and multiple wavelength radiation.

We demonstrated the effect of picosecond multi-pulse burst pumping regime on the steady SRS process. A theoretical model of the interaction between the multi-pulse burst and the Raman active molecule vibration mode was established. The simulation results revealed that the multi-pulse burst regime can enhance the attenuated vibration amplitude and prolong the vibration duration, which compensates the weakened oscillation to return the natural frequency and thereby improves the Raman gain. A picosecond multi-pulse pump KGW crystal comparative experiment was designed, and the results showed that the multi-pulse burst regime can improve the Raman gain of picosecond pulse compared with the single pulse regime, which is manifested as the reduction of the Raman threshold and the increase of the Raman conversion efficiency. The experiment results agree with the theoretical analysis. A 1 kHz 1 064 nm picosecond multi-pulse bursts pump KGW Raman laser was achieved. Based on the three sub-pulses bursts pumping regime, the Raman laser obtained the maximum Stokes average power of 1.39 W, the maximum Stokes conversion efficiency of 29.6% for the 768 cm^–1 vibrational mode, and the maximum Stokes average power of 1.38 W, the maximum Stokes conversion efficiency of 25.7% for the 901 cm^–1 vibrational mode. Meanwhile, the Raman spectra of the first- to fourth-order anti-Stokes lines and the first- to fourth-order Stokes lines for both the vibrational modes of KGW crystal were achieved, which covers the range of 800-1 700 nm. The multi-pulse bursts pumping scheme can present a positive impact on the SRS process, which is beneficial to attain the simultaneous output of high energy and multi-wavelength Raman radiations.