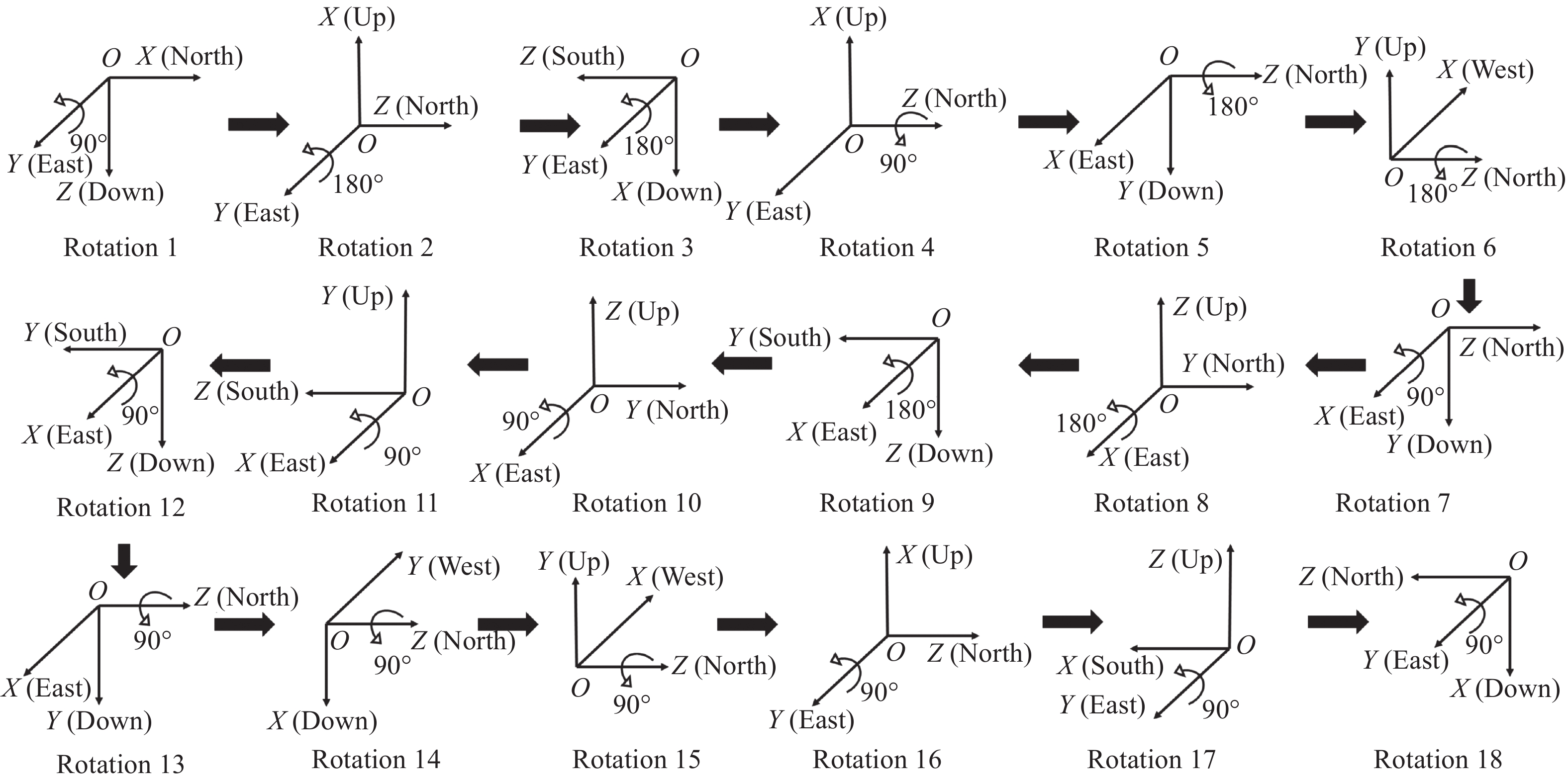
Zichao Wang, Huiying Fan, Yuanping Xie, Hui Luo, Xudong Yu. System-level calibration method for complex error coefficients of strapdown inertial navigation system[J]. Infrared and Laser Engineering, 2022, 51(7): 20210499
Search by keywords or author
- Infrared and Laser Engineering
- Vol. 51, Issue 7, 20210499 (2022)
Abstract
Keywords
| (1) |
View in Article
| (2) |
View in Article
| (3) |
View in Article
| (4) |
View in Article
| (5) |
View in Article
| (6) |
View in Article
| (7) |
View in Article
| (8) |
View in Article
| (9) |
View in Article
| (10) |
View in Article
Set citation alerts for the article
Please enter your email address



