【AIGC One Sentence Reading】:We observed multiple BICs in a hexagonal photonic crystal slab, split by symmetry breaking, with high-Q demonstrated experimentally in the near infrared.
【AIGC Short Abstract】:This work demonstrates theoretically and experimentally multiple bound states in the continuum (BICs) in a hexagonal photonic crystal slab. Symmetry breaking splits merging BICs and retains ultrahigh Q-factors for others. Four high-Q quasi-BICs are observed in the near infrared, with potential applications in nonlinear optics and multiband sensing.
Note: This section is automatically generated by AI . The website and platform operators shall not be liable for any commercial or legal consequences arising from your use of AI generated content on this website. Please be aware of this.
Abstract
Bound states in the continuum (BICs) open up a unique avenue of enhancing light–matter interactions due to their extreme field confinement and infinite quality () factors. Although tremendous progress has been made in the past 10 years, the majority of previous works focused on either a single BIC or dual BICs. In this work, we present both theoretical investigation and experimental demonstration on multiple BICs in a photonic crystal slab with a hexagonal lattice. All of these BICs at -point can be categorized as symmetry-protected (SP) BICs. Furthermore, two BICs belong to merging BICs with topological charges . Breaking the structural symmetry will split these BICs with into two accidental BICs with . While the other two are different from the former two, the -factors of both modes at the -point retain a stably ultrahigh value () when the circular hole is transformed into a rotated elliptical hole with different size ratios of semi-long and semi-short axes. In addition, the -factors of the latter two BICs decrease rapidly with , indicating that the quasi-BICs become accessible at an ultra-small incident angle. We also show that the -factors of the former two BICs exhibit different dependence on the asymmetry parameters, suggesting a viable way of realizing high- resonances at multi-wavelengths. Finally, we presented experimental demonstration of four high- quasi-BICs at four different wavelengths in the near infrared by fabricating a series of photonic crystal slabs made of rotated elliptical holes and characterizing their reflection spectra. We showed that most of the measured -factors are above 1000 for four quasi-BICs, and the highest one can reach 16,764. Our results may find promising applications in sum-frequency generation, four-wave mixing, multiband sensing, lasing, etc.1. INTRODUCTION
Bound states in the continuum (BICs) have received increasing attention in recent years, because they suggest a unique route of boosting light–matter interaction. BICs exist as bound states of the system but embed within the radiation continuum [1–6]. They possess infinite -factors and exhibit no radiation channels to exchange energy with the outside. BICs cannot be accessed by any excitation sources because they are completely decoupled from the exterior environment. In the real applications, it is necessary to introduce perturbations [7–10] to transform BICs into quasi-BICs with finite and high -factors [11–15]. The occurrence of quasi-BICs is always accompanied by the giant field enhancement within and around the structures. Thanks to the extreme field confinement and high -factor enabled by quasi-BICs, they have promised many exciting applications, such as lasing [16–19], sensing [20–23], strong coupling [24–28], and nonlinear harmonic generations [13,29–33]. Nevertheless, most research works reported so far focused on either a single BIC [12,13,34–37] or dual BICs [38–40]. For some practical applications, such as multiband biosensing [41], sum-frequency generation [42,43], and four-wave mixing [44,45], it is highly desired to simultaneously support multiple BICs at several targeted wavelengths in the same structure.
In this work, we report the observation of multiple BICs in silicon photonic crystal slabs with a honeycomb lattice in theory and experiment. We show that four symmetry-protected BICs carrying different topological charges [5,6,46–48] ( and ) can be simultaneously supported in the same structure, and their -factors display drastically different dependence on the asymmetry parameters including structural asymmetry and oblique incidence. We also show that for two BICs with the -factors of quasi-BICs decrease at different rates when symmetry breaking is introduced along different directions, suggesting a unique way of tailoring -factors of quasi-BICs. To confirm the theoretical findings, we fabricate photonic crystal slabs and characterize these high- resonances via a home-made cross-polarization measurement system. We indeed found that there are four high- quasi-BICs at four different wavelengths. The measured -factors of these quasi-BICs are above 1000, and the maximum one is up to 16,764. Our results hold great promise in applications requiring multiple high- resonances, such as four-wave mixing, lasing, and biosensing.
2. RESULTS AND DISCUSSION
While most previous experimental studies on the excitation of a single or dual quasi-BICs build upon a metasurface or photonic crystal slab with a square lattice, we focus on the photonic crystal slab (PCS) with a hexagonal lattice that is less explored for high- quasi-BICs. Different from previous works with symmetry, such a honeycomb structure follows symmetry and thus supports multiple BICs with high topological charges. Without loss of generality, we consider a freestanding silicon PCS with a hexagonal lattice in Fig. 1(a), whose unit cell is made of a circular air hole with radius of . The lattice constant is . The refractive index of silicon is set as . The thickness of silicon slab is . The band structure of such a photonic crystal slab is presented in Figs. 1(b) and 1(c).
Sign up for Photonics Research TOC. Get the latest issue of Photonics Research delivered right to you!Sign up now
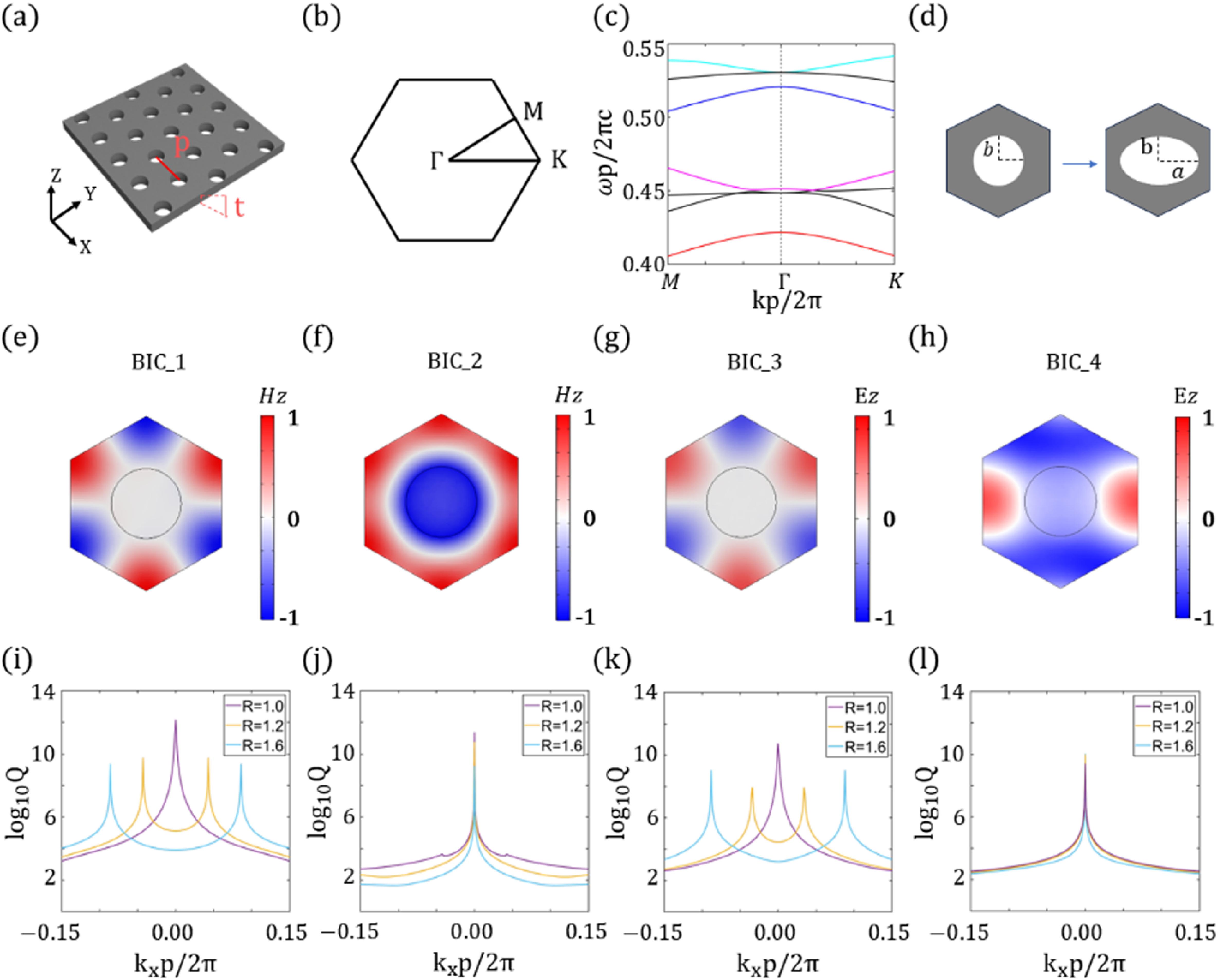
Figure 1.(a) Scheme of a triangular-lattice PCS. (b) Schematic illustration of first Brillouin zone of the PCSs. (c) Calculated band structure of PCSs. BIC-1, BIC-2, BIC-3, and BIC-4 at the point are indicated by the red, pink, blue, and light blue lines, respectively. (d) Cross section of the PCSs. The radius of the circle hole is . The semi-long axis and semi-short axis radii of the ellipse are and , respectively. (e)–(h) Eigen field profiles of BIC-1, BIC-2, BIC-3, and BIC-4. (i)–(l) -factors of BIC-1, BIC-2, BIC-3, and BIC-4 in the direction.
Here, we focus on four lowest-order BICs, whose eigenfield distributions are shown in Figs. 1(e)–1(h). Unlike the low-order BICs carrying topological charges in metasurfaces or PCSs with symmetry, two of the lowest-order BICs (BIC-1 and BIC-3) at the point in a PCS with symmetry carry topological charges . If this circular hole is transformed into an elliptical hole, lattice symmetry evolves from into . Consequently, such BICs will be split into two accidental BICs at off-Γ point, each of which carries a topological charge . As shown in Fig. 1(d), the size ratio of the elliptical hole is defined as , where and are the semi-long and semi-short axes of the ellipse, respectively. It can be found from Figs. 1(i) and 1(k) that two BICs appear at off-Γ point when the size ratio deviates from . Moreover, these BICs become more and more far away from the -point with size ratio increasing.
Further analysis on the -factors of BIC-1 and BIC-3 versus indicates that these two BICs belong to merging BICs [6,46,47,49–52] because it follows . On the other hand, two accidental BICs follow the inversely quadratic rule, , where is the wave vector of the accidental BIC. Thus, such natural merging BICs at the Γ-point arising with symmetry suggest a viable way of realizing ultrahigh high- resonances. This is different from some merging BICs in a PCS or metasurface with a square (or hexagonal) lattice which requires carefully tuning the geometry parameters [46,50,53–55]. The splitting behavior of BICs is also confirmed in -factor mapping in Figs. 2(a) and 2(c). Meanwhile, polarization states are given in the same figures, verifying that a topological charge splits into two charges with .
Figure 2.Simulated polarization vectors around the BICs with the as the background color. (a)–(d) Correspond respectively to BIC-1, 2, 3, and 4. Left: for triangular-lattice PCSs with circular holes. Right: for triangular-lattice PCSs with elliptical holes ().
However, BIC-2 and BIC-4 exhibit different trends from the former two BICs. From Figs. 1(j) and 1(l), it can be seen that the nature of these two BICs at the -point is preserved no matter how the size ratio varies because the inverse symmetry is kept for these two modes. Nevertheless, these BICs are converted into quasi-BICs with high- factors if a small is introduced. The -factors of quasi-BICs satisfy the inversely quadratic rule, which is . In other words, a small incident angle can induce the excitation of quasi-BICs. Besides, we also calculate the -factors mapping in the momentum space. For BIC-2, except for BICs located at the -point, there are another six BICs around it. They are respectively distributed at the corner of a hexagon. Properly choosing the lattice constants can merge these six BICs at the -point. Topological charge calculations show that a BIC at the -point carries a topological charge . Another six BICs carry topological charges . When the size ratio increases from 1 to 1.2, only three BICs are kept. Besides one locating at the -point, another two are located along the axis. In contrast, for the case of BIC-4, as shown in Fig. 2(d), BIC is pinned at the -point. However, it is interesting to note that such a BIC carries a topological charge for while the topological charge becomes due to the lattice symmetry transition from to . Here, it is worth pointing out that BIC-4 belongs to the degenerate BICs [7,56], which is the unique property of BICs in a PCS with a hexagonal lattice. By applying lattice deformation and structural breaking, one can remove degeneracy. Also, multiple topological half charges can be generated via introducing different types of perturbation.
Note that the aim of this work is to realize multiple high- resonances at normal incidence; thus we move to investigate how the -factors of the quasi-BICs at the -point depend on the asymmetry parameter [53,54] defined as . Here, we choose three types of structures to study the behaviors of -factors of BICs, where the angles between the semi-long axis and axis are 0°, 45°, and 90° [Figs. 3(a)–3(c)]. We first consider the case of BIC-1 and BIC-3 because they are converted into quasi-BICs when the symmetry breaking is induced. The relevant results are plotted in Figs. 3(d)–3(i). For BIC-1, from Figs. 3(d)–3(f) one can observe that the -factor of quasi-BICs does not follow the rigorous inverse-quadratic rule. By fitting the curves of versus , the slopes are , and , respectively. This suggests a feasible way of realizing ultrahigh- resonances by simply rotating the elliptical hole. A similar conclusion can be drawn to BIC-3. Unlike BIC-1 and BIC-3, both BIC-2 and BIC-4 at the -point exhibit weak dependence on the asymmetry parameter , as shown in Figs. 4(a)–4(f).
Figure 3.(a)–(c) Schematics of triangular-lattice PCSs slab with circular holes (). (d)–(f) Q-factors versus at point in the mode 1 (). (g)–(i) Q-factors versus at point in the mode 3 ().
Figure 4.(a)–(c) Q-factors versus at point in the mode 2 (). (d)–(f) Q-factors versus at point in the mode 4 ().
3. EXPERIMENTAL DEMONSTRATION
Next, we demonstrated experimentally that multiple high- resonances can be achieved based on such a PCS with a hexagonal lattice. The home-built microscope spectroscopy system based on cross-polarization measurement is applied to characterize these high- resonances. Specifically, a super-continuum laser is used as a light source to provide a broad spectrum ranging from 430 to 2400 nm, and the output light is collected by a spectrometer with a theoretical resolution of 0.05 nm to detect high- resonances. Nearly normal incidence is applied to the structure. The laser spot size is larger than the dimensions of the whole metasurface to mimic the normal incidence. Both the incident angle and the detection angle are close to 0°. Two orthogonal polarizers are placed in the incidence path and detection path to eliminate the scattering from background and thus improve the signal-to-noise ratio (see Fig. 5).
Figure 5.Schematic illustration of experimental setup based on cross-polarization measurement.
We manufacture a series of triangular-lattice PCSs with elliptical holes based on silicon on insulator substrate (). The whole structure is schematically shown in Fig. 6(a). The lattice constants of triangular-lattice PCSs are . The elliptical holes are at the center of triangular-lattice structures with different semi-long axis from 185 to 265 nm when we fix semi-short axis . The angle between the semi-long axis and the horizontal orientation is fixed as . Figure 6(b) shows the scanning electron microscopy (SEM) image of a fabricated PCS. Figure 6(c) shows a represented scattering spectrum of the PCS with . Applying the standard Fano fitting process [57] gives us both the resonance wavelength and line width of the resonances . The -factor for such a structure is 16,764. A similar procedure can be applied on the scattering spectrum of the PCS with different [see Fig. 6(d)] to retrieve the resonance wavelengths and -factors of quasi-BIC-1. Excellent agreement can be found between the simulation and measurement, as shown in Figs. 6(e) and 6(f). When increases from 20 to 100 nm, its -factor decreases from 16,764 to 1151. Note that during simulation the refractive index of substrate is set as . Such a high- resonance is good enough for many applications, such as lasing and nonlinear harmonic generations. We shall expect that the -factor of quasi-BIC-1 can be further improved if an even small is applied. Except for high- resonances around 1500 nm, quasi-BIC-3 featured as Fano resonance at 1260 nm is also observed. The relevant scattering spectra are plotted in Fig. 6(g). Following the similar analysis, we indeed found that the resonance wavelength shows blue shift and -factor decreases as the difference between semi-long axis and semi-short axis increases. The maximum -factor of quasi-BIC-3 is 7107 at .
Figure 6.(a) Schematic illustration of a photonic crystal slab under plane wave illumination. (b) SEM image of a PCS. The scale is 400 nm. (c) Scattering spectra of PCSs with . (d) Scattering spectra of PCSs while a quasi-BIC based on BIC-1 is excited in this wavelength window. (e), (f) Retrieved resonance wavelengths (e) and -factors (f) of resonance based on mode 1 at different . (g) Scattering spectra of PCS while a quasi-BIC based on BIC-3 is excited in this wavelength window. (h), (i) Retrieved resonance wavelengths (h) and -factors (i) of resonance based on mode 3 at different .
Although the -factors of BIC-2 and BIC-4 at -point are maintained above an ultrahigh value no matter how the elliptical hole is rotated, these two BICs are converted into quasi-BICs with high -factors even when a small incident angle is applied. In real measurement, the incident light is not perfectly collimated. Inevitably, there will always be a slight oblique incidence angle. Thus, we also observe another two high- resonances originated from BIC-2 and BIC-4. The relevant scattering spectra are presented in Figs. 7(a) and 7(b). The retrieved resonance wavelength and -factors of two resonances are shown in Figs. 7(c) and 7(d). Different from BIC-1 and BIC-3, both -factors show mild dependence on , and their values are maintained above 1000. It is worth noting that during simulation the incident angle is set within a range between 1° and 3° since the calculated -factors are sensitive to the incident angle. The incident angle in measurement for these two modes shall fall within the range.
Figure 7.(a) Scattering spectra of PCSs while a quasi-BIC based on BIC-2 is excited in this wavelength window. (b) Scattering spectra of PCSs while a quasi-BIC based on BIC-4 is excited in this wavelength window. (c), (d) Retrieved resonance wavelengths (c) and -factors (d) of resonance based on mode 2 and mode 4 at different . In the legends of (c) and (d), 0.01 and 0.02 represent and , which correspond to angles of approximately 1° and 3°, respectively.
4. CONCLUSION
In conclusion, we report multiple high- resonances by leveraging BICs in a PCS with a hexagonal lattice. We show that two of BICs belong to merging BICs with topological charges while the other two are normal symmetry protected BICs. By breaking the lattice symmetry from to , the former two merging BICs are split into two accidental BICs, respectively. Meanwhile, the nature of another two BICs is preserved. We also study the -factors of quasi-BICs under different perturbation and find that the -factors of the former two quasi-BICs at -point versus asymmetry parameters exhibit different slopes for PCSs with rotated elliptical holes, suggesting a convenient way of achieving high- resonances at normal incidence. On the contrary, the latter two SP BICs have a stably high -factor above . However, they are very sensitive to the incident angle. A small incident angle can induce significant reduction on their -factors. Finally, we validate the existence of multiple high- resonances by manufacturing a series of triangular-lattice samples with elliptical holes. Four high- resonances with are simultaneously realized in a PCS. Both the measured resonance wavelengths and -factors of four quasi-BICs match well with the theoretical prediction. The largest -factor is up to 16,764. Our results may find promising applications in developing high-performance devices that require multiple high- resonances, such as sum-frequency generation and high-quality quantum light source.
References
[1] C. W. Hsu, B. Zhen, A. D. Stone. Bound states in the continuum. Nat. Rev. Mater., 1(2016).
[2] L. Huang, Y. K. Chiang, S. Huang. Sound trapping in an open resonator. Nat. Commun., 12, 4819(2021).
[3] L. Huang, L. Xu, D. A. Powell. Resonant leaky modes in all-dielectric metasystems: fundamentals and applications. Phys. Rep., 1008, 1-66(2023).
[4] J. Wang, P. Li, X. Zhao. Optical bound states in the continuum in periodic structures: mechanisms, effects, and applications. Photonics Insights, 3, R01(2024).
[5] B. Zhen, C. W. Hsu, L. Lu. Topological nature of optical bound states in the continuum. Phys. Rev. Lett., 113, 257401(2014).
[6] T. Yoda, M. Notomi. Generation and annihilation of topologically protected bound states in the continuum and circularly polarized states by symmetry breaking. Phys. Rev. Lett., 125, 053902(2020).
[7] C. F. Doiron, I. Brener, A. Cerjan. Realizing symmetry-guaranteed pairs of bound states in the continuum in metasurfaces. Nat. Commun., 13, 7534(2022).
[8] L. Huang, S. Li, C. Zhou. Realizing ultrahigh‐Q resonances through harnessing symmetry‐protected bound states in the continuum. Adv. Funct. Mater., 34, 2309982(2024).
[9] K. Koshelev, S. Lepeshov, M. Liu. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett., 121, 193903(2018).
[10] X. Wang, J. Wang, X. Zhao. Realizing tunable evolution of bound states in the continuum and circularly polarized points by symmetry breaking. ACS Photonics, 10, 2316-2322(2022).
[11] C. Cui, C. Zhou, S. Yuan. Multiple Fano resonances in symmetry-breaking silicon metasurface for manipulating light emission. ACS Photonics, 5, 4074-4080(2018).
[12] K. Koshelev, Y. Tang, K. Li. Nonlinear metasurfaces governed by bound states in the continuum. ACS Photonics, 6, 1639-1644(2019).
[13] L. Xu, K. Z. Kamali, L. Huang. Dynamic nonlinear image tuning through magnetic dipole quasi‐BIC ultrathin resonators. Adv. Sci., 6, 1802119(2019).
[14] H. Zhong, L. Huang, S. Li. Toroidal dipole bound states in the continuum in asymmetric dimer metasurfaces. Appl. Phys. Rev., 11, 031404(2024).
[15] M. Zhou, S. You, J. Liu. Selective perturbation of eigenfield enables high-q quasi-bound states in the continuum in dielectric metasurfaces. ACS Photonics, 11, 2413-2421(2024).
[16] S. I. Azzam, K. Chaudhuri, A. Lagutchev. Single and multi‐mode directional lasing from arrays of dielectric nanoresonators. Laser Photonics Rev., 15, 2000411(2021).
[17] A. Kodigala, T. Lepetit, Q. Gu. Lasing action from photonic bound states in continuum. Nature, 541, 196-199(2017).
[18] V. Mylnikov, S. T. Ha, Z. Pan. Lasing action in single subwavelength particles supporting supercavity modes. ACS Nano, 14, 7338-7346(2020).
[19] M. Wu, S. T. Ha, S. Shendre. Room-temperature lasing in colloidal nanoplatelets via Mie-resonant bound states in the continuum. Nano Lett., 20, 6005-6011(2020).
[20] G. Li, Y. Liu. Homogeneous and significant near‐field enhancement in all‐dielectric metasurfaces for sensing applications. Adv. Opt. Mater., 12, 2400425(2024).
[21] Q. Ma, Q. R. Hong, X. X. Gao. Smart sensing metasurface with self-defined functions in dual polarizations. Nanophotonics, 9, 3271-3278(2020).
[22] J. Qin, S. Jiang, Z. Wang. Metasurface micro/nano-optical sensors: principles and applications. ACS Nano, 16, 11598-11618(2022).
[23] A. Tittl, A. Leitis, M. Liu. Imaging-based molecular barcoding with pixelated dielectric metasurfaces. Science, 360, 1105-1109(2018).
[24] I. A. Al‐Ani, K. As’ Ham, L. Huang. Enhanced strong coupling of TMDC monolayers by bound state in the continuum. Laser Photonics Rev., 15, 2100240(2021).
[25] I. A. Al‐Ani, K. As’ Ham, L. Huang. Strong coupling of exciton and high‐Q mode in all‐perovskite metasurfaces. Adv. Opt. Mater., 10, 2101120(2022).
[26] K. Koshelev, S. Sychev, Z. F. Sadrieva. Strong coupling between excitons in transition metal dichalcogenides and optical bound states in the continuum. Phys. Rev. B, 98, 161113(2018).
[27] M. Qin, S. Xiao, W. Liu. Strong coupling between excitons and magnetic dipole quasi-bound states in the continuum in WS2-TiO2 hybrid metasurfaces. Opt. Express, 29, 18026-18036(2021).
[28] H. Zhou, M. Qin, H. Xu. Photonic spin-controlled self-hybridized exciton-polaritons in WS2 metasurfaces driven by chiral quasibound states in the continuum. Phys. Rev. B, 109, 125201(2024).
[29] N. Bernhardt, K. Koshelev, S. J. White. Quasi-BIC resonant enhancement of second-harmonic generation in WS2 monolayers. Nano Lett., 20, 5309-5314(2020).
[30] L. Carletti, S. S. Kruk, A. A. Bogdanov. High-harmonic generation at the nanoscale boosted by bound states in the continuum. Phys. Rev. Res., 1, 023016(2019).
[31] I. Volkovskaya, L. Xu, L. Huang. Multipolar second-harmonic generation from high-Q quasi-BIC states in subwavelength resonators. Nanophotonics, 9, 3953-3963(2020).
[32] G. Zograf, K. Koshelev, A. Zalogina. High-harmonic generation from resonant dielectric metasurfaces empowered by bound states in the continuum. ACS Photonics, 9, 567-574(2022).
[33] S. Xiao, M. Qin, J. Duan. Polarization-controlled dynamically switchable high-harmonic generation from all-dielectric metasurfaces governed by dual bound states in the continuum. Phys. Rev. B, 105, 195440(2022).
[34] J. Lee, B. Zhen, S.-L. Chua. Observation and differentiation of unique high-Q optical resonances near zero wave vector in macroscopic photonic crystal slabs. Phys. Rev. Lett., 109, 067401(2012).
[35] S. Li, C. Zhou, T. Liu. Symmetry-protected bound states in the continuum supported by all-dielectric metasurfaces. Phys. Rev. A, 100, 063803(2019).
[36] V. R. Tuz, V. V. Khardikov, A. S. Kupriianov. High-quality trapped modes in all-dielectric metamaterials. Opt. Express, 26, 2905-2916(2018).
[37] C. Zhou, L. Huang, R. Jin. Bound states in the continuum in asymmetric dielectric metasurfaces. Laser Photonics Rev., 17, 2200564(2023).
[38] Y. Cai, Y. Huang, K. Zhu. Symmetric metasurface with dual band polarization-independent high-Q resonances governed by symmetry-protected BIC. Opt. Lett., 46, 4049-4052(2021).
[39] L. Cong, R. Singh. Symmetry‐protected dual bound states in the continuum in metamaterials. Adv. Opt. Mater., 7, 1900383(2019).
[40] S. Zhang, M. Zong, Y. Liu. Independent dual‐band bound states in the continuum supported by double asymmetric periodic gratings in germanium‐based structure. Laser Photonics Rev., 18, 2301206(2024).
[41] Z. Vafapour, H. Ghahraloud, A. Keshavarz. The potential of refractive index nanobiosensing using a multi-band optically tuned perfect light metamaterial absorber. IEEE Sens. J., 21, 13786-13793(2021).
[42] R. Camacho-Morales, L. Xu, H. Zhang. Sum-frequency generation in high-Q GaP metasurfaces driven by leaky-wave guided modes. Nano Lett., 22, 6141-6148(2022).
[43] A. G. Lambert, P. B. Davies, D. J. Neivandt. Implementing the theory of sum frequency generation vibrational spectroscopy: a tutorial review. Appl. Spectrosc. Rev., 40, 103-145(2005).
[44] M. Cronin-Golomb, B. Fischer, J. White. Theory and applications of four-wave mixing in photorefractive media. IEEE J. Quantum Electron., 20, 12-30(1984).
[45] J. W. You, Z. Lan, N. C. Panoiu. Four-wave mixing of topological edge plasmons in graphene metasurfaces. Sci. Adv., 6, eaaz3910(2020).
[46] M. Kang, L. Mao, S. Zhang. Merging bound states in the continuum by harnessing higher-order topological charges. Light Sci. Appl., 11, 228(2022).
[47] M. Kang, S. Zhang, M. Xiao. Merging bound states in the continuum at off-high symmetry points. Phys. Rev. Lett., 126, 117402(2021).
[48] W. Ye, Y. Gao, J. Liu. Singular points of polarizations in the momentum space of photonic crystal slabs. Phys. Rev. Lett., 124, 153904(2020).
[49] P. Hu, J. Wang, Q. Jiang. Global phase diagram of bound states in the continuum. Optica, 9, 1353-1361(2022).
[50] J. Jin, X. Yin, L. Ni. Topologically enabled ultrahigh-Q guided resonances robust to out-of-plane scattering. Nature, 574, 501-504(2019).
[51] X. Qi, J. Wu, F. Wu. Steerable merging bound states in the continuum on a quasi-flatband of photonic crystal slabs without breaking symmetry. Photonics Res., 11, 1262-1274(2023).
[52] G. Sun, Y. Wang, Y. Li. Tailoring topological nature of merging bound states in the continuum by manipulating structure symmetry of the all-dielectric metasurface. Phys. Rev. B, 109, 035406(2024).
[53] Z. Liu, Y. Xu, Y. Lin. High-Q quasibound states in the continuum for nonlinear metasurfaces. Phys. Rev. Lett., 123, 253901(2019).
[54] Z. Zhang, E. Bulgakov, K. Pichugin. Super quasibound state in the continuum. Phys. Rev. Appl., 20, L011003(2023).
[55] Z. Zhang, F. Qin, Y. Xu. Negative refraction mediated by bound states in the continuum. Photonics Res., 9, 1592-1597(2021).
[56] X. Zhao, J. Wang, W. Liu. Spin-orbit-locking chiral bound states in the continuum. Phys. Rev. Lett., 133, 036201(2024).
[57] A. E. Miroshnichenko, S. Flach, Y. S. Kivshar. Fano resonances in nanoscale structures. Rev. Mod. Phys., 82, 2257-2298(2010).

![]()
![]()
![]()
![]()
![]()
![]()



 AI Video Guide
AI Video Guide  AI Picture Guide
AI Picture Guide AI One Sentence
AI One Sentence


