Shuangli Li, Lujun Huang, Haozong Zhong, Minghao Ning, Ling-En Zhang, Yaling Yin, Ya Cheng, Lin Li, "Observation of multiple quasi-bound states in the continuum by symmetry breaking in a photonic crystal slab," Photonics Res. 13, 968 (2025)
- Photonics Research
- Vol. 13, Issue 4, 968 (2025)
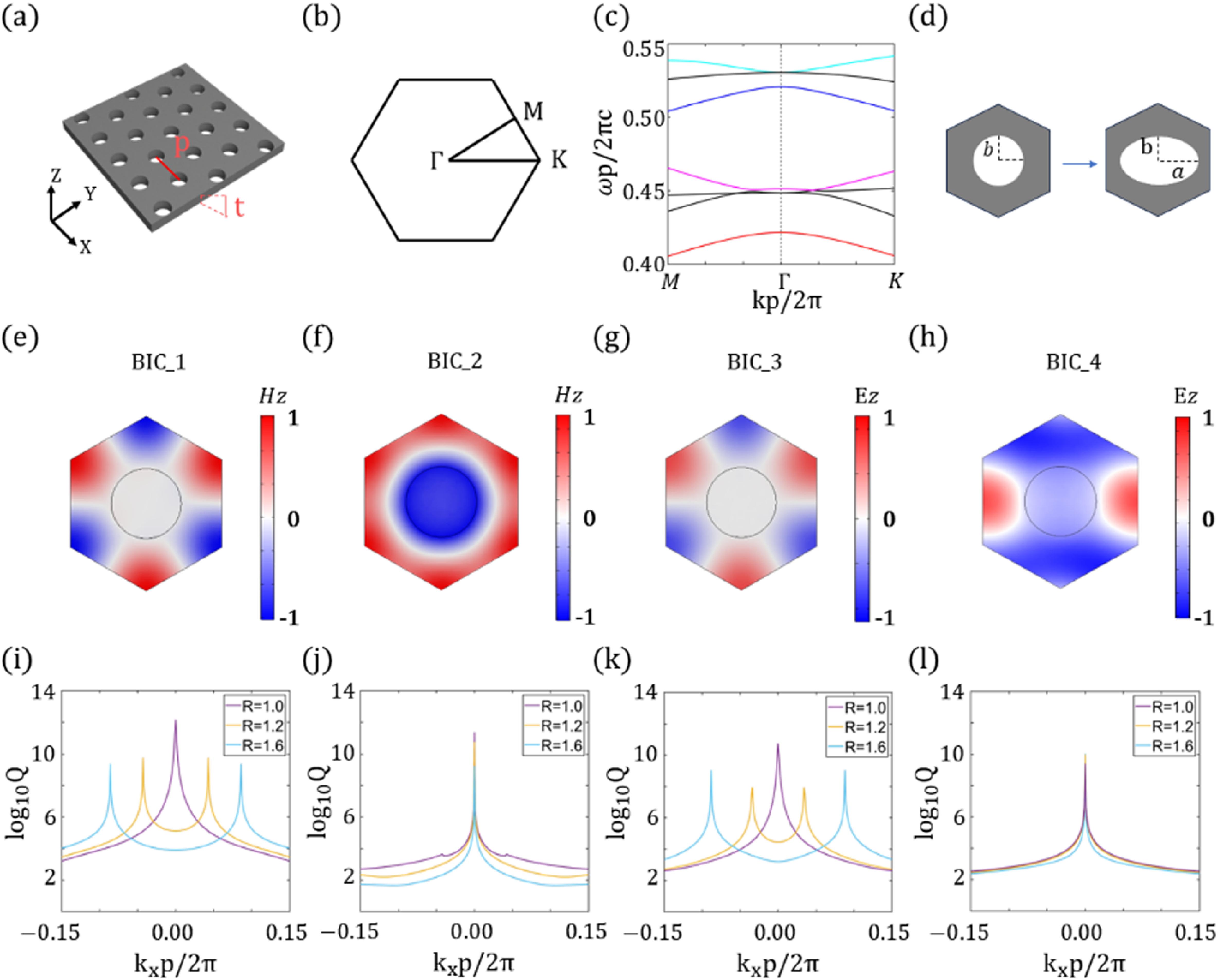
Fig. 1. (a) Scheme of a triangular-lattice PCS. (b) Schematic illustration of first Brillouin zone of the PCSs. (c) Calculated band structure of PCSs. BIC-1, BIC-2, BIC-3, and BIC-4 at the Γ b a b Q Γ -K
Fig. 2. Simulated polarization vectors around the BICs with the log 10 Q R = 1.2
Fig. 3. (a)–(c) Schematics of triangular-lattice PCSs slab with circular holes (θ = 0 ° , 45 ° , 90 ° Q -factors versus α = a − b b Γ θ = 0 ° , 45 ° , 90 ° Q -factors versus α = a − b b Γ θ = 0 ° , 45 ° , 90 °
Fig. 4. (a)–(c) Q -factors versus α = a − b b Γ θ = 0 ° , 45 ° , 90 ° Q -factors versus α = a − b b Γ θ = 0 ° , 45 ° , 90 °
Fig. 5. Schematic illustration of experimental setup based on cross-polarization measurement.
Fig. 6. (a) Schematic illustration of a photonic crystal slab under plane wave illumination. (b) SEM image of a PCS. The scale is 400 nm. (c) Scattering spectra of PCSs with Δ = a − b = 20 nm Q Δ = a − b Q Δ = a − b
Fig. 7. (a) Scattering spectra of PCSs while a quasi-BIC based on BIC-2 is excited in this wavelength window. (b) Scattering spectra of PCSs while a quasi-BIC based on BIC-4 is excited in this wavelength window. (c), (d) Retrieved resonance wavelengths (c) and Q Δ = a − b ( k x , k y ) = ( 0.01 2 π p , 0.01 2 π p ) ( k x , k y ) = ( 0.02 2 π p , 0.02 2 π p )
Set citation alerts for the article
Please enter your email address
© Copyright 2018-2021 | Chinese Laser Press. All Rights Reserved 沪ICP备15018463号-20