In the past few decades, the capacity of optical communication systems has experienced explosive growth, attributed to the emergence of coherent detection, erbium-doped fiber amplifiers (EDFAs), and advanced digital signal processing algorithms^[1–3]. As the foundation of the current optical network, silica single-mode fibers (SMFs) are approaching their capacity limit due to inherent Kerr nonlinear effects^[4,5]. Recently, the application of hollow-core fibers (HCFs) in optical transmission systems has undergone intensive investigation. The HCF, featuring a gas-filled center core, presents advantages over conventional SMFs, including reduced nonlinearity, lower chromatic dispersion, and lower latency^[6,7]. Among various types of hollow-core fibers, the nested anti-resonant nodeless fiber (NANF), which utilizes nested anti-resonant tubes to effectively confine light to propagate within the core of the fiber, has become a research hotspot for its intrinsically lower nonlinearity and fiber loss compared to the hollow-core photonic bandgap fiber. Consequently, broadband transmission, incorporated with the wavelength division multiplexing (WDM) technology, stands out as one of the most significant application fields for the NANF. Notable achievements in large-capacity transmission over an HCF have been reported^[8–10]. In Ref. [8], a successful demonstration of up to 800 Gbps transmission covering C- and L-bands over $\sim 1\mathrm{km}$ NANF was achieved using the direct detection scheme. As for the coherent system, Ref. [9] presented a remarkable 61-channel transmission, delivering 32-GBaud 16-ary quadrature amplitude modulation (16QAM) with a total capacity of 15.6 Tbit/s. However, these experiments primarily evaluated the performance of low-order modulation format signals (e.g.,  PAM4, QPSK, and 16QAM), which lack spectral efficiency.

As is known, the combination of the high-order QAM modulation format and the probabilistic shaping (PS) technology is significant for improving the spectrum efficiency and narrowing the gap to the Shannon limit^[11]. However, the high-order QAM signal is sensitive to the phase noise, especially when combined with the PS technology^[12,13]. The nonuniform probability distribution of the PS signals renders the internal constellation with higher probabilities more likely to fall near the decision boundary. This phenomenon will affect the correct decision of the PS symbols, thus degrading the performance of certain carrier phase estimation (CPE) algorithms. In Ref. [14], a robust and flexible two-stage CPE algorithm combining principal component-based phase estimation (PCPE) and blind phase search (BPS) was introduced for the PS-QAM format. However, the probability-unaware principle makes it a sub-optimal CPE algorithm for PS signals. A maximum-probability-directed blind phase search (MPD-BPS), derived from the known BPS for PS signals, was proposed to obtain an average 0.13-dB signal-to-noise (SNR) gain compared to traditional BPS. However, the performance gain is relatively limited^[15]. Therefore, introducing the PS-optimal CPE algorithm into the PS-assisted NANF transmission systems is meaningful.

In this work, we propose a novel maximum a posteriori probability detection-based decision-directed CPE (MAP-DDCPE) to enable PS-assisted broadband NANF transmission. Different from the aforementioned CPE algorithms, MAP-DDCPE is capable of tracking the tiny phase disturbances at low complexity due to the recursive single-tap phase estimation. Meanwhile, it utilizes maximum a posteriori probability (MAP) detection to obtain the correct error information for the PS symbols, which is essential for recursive phase estimation. To the best of our knowledge, this is the first time that the probability-aware MAP detection has been introduced into DDCPE, which tends to solve conflicts between the PS formant and current CPE. With the proposed digital signal processing (DSP) algorithm, the 96-channel transmission delivering the 40-GBaud polarization division multiplexing (PDM) PS-64QAM signals with the entropy of 5.9-bits/symbol (PS-64QAM-5.9) over the 2-km NANF is presented. Considering the cost of soft-decision forward error correction (SD-FEC), the capacity of the broadband NANF transmission is beyond 35-Tbps. To illustrate the advantages of the proposed solution more effectively, the additional experimental results include (1) comparing the performance of different CPE algorithms (PCPE, MPD-BPS, and MAP-DDCPE) after NANF transmission in shallow, moderate, and strong shaping cases and (2) comparing the tolerance for injected optical power between NANF and standard SMF (SSMF).

Different from the aforementioned CPE algorithms, which require a time window, the proposed recursive MAP-DDCPE with the single tap is superior in the phase-tracking ability and calculation efficiency^[16]. In the MAP-DDCPE, the received symbol at the $i$th interval $y_{{\mathrm{MAP}}_i}$ is firstly multiplied by the unit phase rotation factor ${\phi }_i$, which is expressed as ${\phi }_i=e^{-j{\widehat{\theta }}_{{\mathrm{DDCPE}}_i}}$, to compensate for the phase noise. Here, ${\widehat{\theta }}_{{\mathrm{DDCPE}}_i}$ denotes the estimated phase, which is obtained in the previous interval by the recursive DDCPE. Then, the rotated symbol, denoted as $y_{r_i}$, is decided to the nearest QAM constellation $d_{{\mathrm{MAP}}_i}$. To avoid the wrong detection aggravated by the PS technique, we adopt the probability-aware MAP detection scheme, which is expressed as $$d_{{\mathrm{MAP}}_i}=\underset{x_k}{\mathrm{argmin}}\{{|y_{{\mathrm{MAP}}_i}-x_k|}^2-N_0\ln [p_x(x_k)]\},$$(1)where $N_0$ denotes the noise variance, which can be obtained by the noise power of pilot symbols, $x_k$ denotes the symbol that belongs to the QAM constellation set, and $p_x$ refers to the prior probability of the QAM constellation, which is always known at the receiver. Compared to the commonly used maximum likelihood detection based on the Euclidean distance, the second term in Eq. (1) for MAP detection introduces the prior probability information to the detection. When adopted in the PS-QAM modulation format following nonuniform probability distribution, the MAP detection will expand the decision region of the constellation with the higher occurrence probability^[17]. The changed decision region based on the probability of the constellation renders the PS signals originally located on the decision boundary to fall back within the decision region. Therefore, the PS-suitable MAP detection greatly reduces symbol decision errors caused by an uneven probability distribution, which is essential for the DDCPE.

After MAP detection, the decision error $e_{{\mathrm{MAP}}_i}$ is calculated as $e_{{\mathrm{MAP}}_i}=d_{{\mathrm{MAP}}_i}-y_{r_i}$, which also can be expressed as $e_{{\mathrm{MAP}}_i}=d_{{\mathrm{MAP}}_i}-y_{{\mathrm{MAP}}_i}{e}^{-j{\widehat{\theta }}_{{\mathrm{DDCPE}}_i}}$. In the proposed MAP-DDCPE, the estimated phase ${\widehat{\theta }}_{{\mathrm{DDCPE}}_i}$ is searched using the gradient descent method. The gradient descent algorithm in the MAP-DDCPE can be divided into two steps: (1) Find the gradient. The gradient refers to the direction that minimizes the square error magnitude ${\epsilon }_{{\mathrm{MAP}}_i}={|e_{{\mathrm{MAP}}_i}|}^2$. Therefore, the gradient direction $g_{{\mathrm{MAP}}_i}$ should be opposite with the derivative of the square error magnitude with respect to the estimated phase that can be inferred by substituting $e_{{\mathrm{MAP}}_i}=d_{{\mathrm{MAP}}_i}-y_{r_i}$ and $y_{r_i}=y_{{\mathrm{MAP}}_i}{e}^{-j{\widehat{\theta }}_{{\mathrm{DDCPE}}_i}}$, $$\begin{gathered} g_{{\mathrm{MAP}}_i}=-1\times (\partial {\epsilon }_{{\mathrm{MAP}}_i}/\partial {\widehat{\theta }}_{{\mathrm{DDCPE}}_i}) \\ =-e_{{\mathrm{MAP}}_i}^{\prime }{e}_{{\mathrm{MAP}}_i}^{*}-e_{{\mathrm{MAP}}_i}{(e_{{\mathrm{MAP}}_i}^{*})}^{\prime }=-2\Im \{e_{{\mathrm{MAP}}_i}{y}_{r_i}^{*}\}, \end{gathered}$$(2)where ${(·)}^{*}$ and ${(·)}^{\prime }$ represent the complex conjugate and derivative operation, respectively, $\partial (·)$ denotes the partial derivative function, and $\Im \{·\}$ refers to the imaginary part of the complex number. (2) Update the estimated phase along the gradient. A step-size factor $\mu$ is introduced to balance the speed and precision of the phase tracking. Therefore, the recursive expression of the estimated phase in the DDCPE algorithm is expressed as $${\widehat{\theta }}_{{\mathrm{DDCPE}}_{i+1}}={\widehat{\theta }}_{{\mathrm{DDCPE}}_i}-\mu \Im \{e_{{\mathrm{MAP}}_i}{y}_{r_i}^{*}\}.$$(3)

As a single-tap recursive CPE algorithm, the MAP-DDCPE has excellent phase-tracking ability. We believe the proposed MAP-DDCPE is suitable for high-order PS signals whose performance is investigated in the broadband NANF transmission experiment.

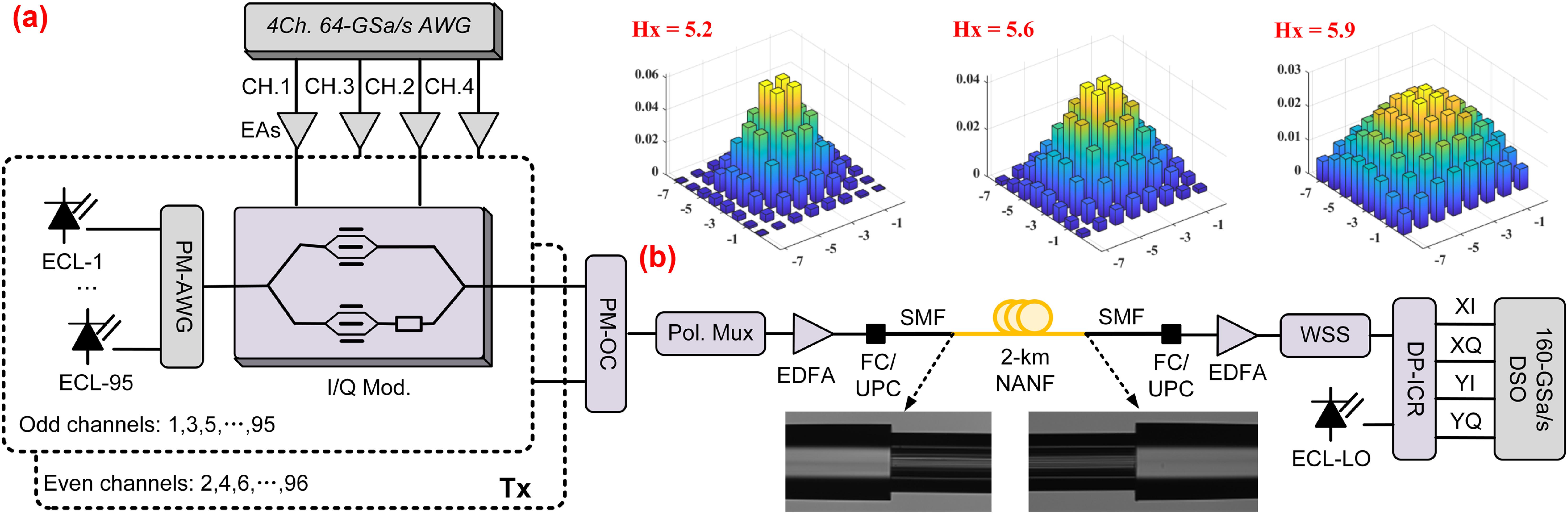
The experimental setup of the 96-channel WDM coherent system is demonstrated in Fig. 1(a). At the transmitter (Tx) end, 96 external cavity lasers (ECLs) operating from 191.45 to 196.2 THz with 50-GHz spacing emit the WDM optical carriers. By adopting the self-heterodyne method, the linewidth of the employed ECLs is measured to be less than 120 kHz. The 96 channels are divided into 48 odd channels (Ch 1, 3, …, 95), corresponding to the ITU-T C15-C62 channels, and 48 even channels (Ch 2, 4, …, 96), corresponding to the ITU-T H14-H61 channels, which are respectively combined by two polarization-maintaining arrayed waveguide gratings (PM-AWG) and then injected into the I/Q modulators (I/Q Mod.) with 35-GHz bandwidth. Two different 40-GBaud baseband PS-64QAM signals are generated by the 64-GSa/s AWG and then boosted by the parallel electrical amplifiers (EAs) to drive the modulator. Next, the two 48-channel modulated optical signals are combined by a polarization-maintaining optical coupler (PM-OC). Before being pre-amplified by the EDFA, the WDM signals are sent to the polarization multiplexer (Pol. Mux.) to generate the PDM signals. The optical delay line (ODL) employed in the Pol. Mux. is around 2 m for decorrelation. Afterward, the 96-channel PDM signals are delivered through the NANF span.

The assembled fiber span comprises a 2032-m NANF and a 6-m SMF for splicing. As depicted in Fig. 1(a), the two ends of the NANF are spliced to the SMF patch cords to incorporate the NANF in an SMF-based optical system, which causes a 0.9-dB splicing loss for each end. The scanning electron microscope (SEM) image and total loss curve of the NANF are demonstrated in Fig. 2(a). The hollow core of the NANF with a 26-µm diameter (maximum inscribed circle tangent to the outer tube) is surrounded by five nested tubes. The diameters of the inner and outer tubes are 16 and 27 µm, respectively. The employed NANF has a wall thickness reaching 1.13 µm. Due to the limitations in the manufacturing process, the fiber parameters, including the diameter and wall thickness, may change within the range of 5% from one fiber end to another. The relatively high wall thickness and structure inhomogeneity leads to a higher loss compared with the work in Ref. [18]. Across the entire C-band, the total loss of the NANF span is lower than 10 dB/km, achieving a minimum loss of 5.215 dB/km at 1551 nm. Moreover, the chromatic dispersion and nonlinear coefficient of the employed NANF in this experiment are $4.42\mathrm{ps}/(\mathrm{nm}*\mathrm{km})$ and $0.007\mathrm{rad}/(\mathrm{W}*\mathrm{km})$ at 1550 nm. The low- and flatten-loss NANF is an important prerequisite for high-speed broadband transmission.

The optical spectra of the 96-channel WDM signal before and after NANF transmission are demonstrated in Fig. 2(b), which is recorded at 0.02-nm resolution. High power consistency is observed across different wavelength channels. After the 2-km NANF transmission, an EDFA with a typical 5-dB noise figure at 1550 nm is adopted to compensate for the NANF loss. The output power of the EDFA is set as 22 dBm. Considering the baud rate of the transmitted signal and the frequency shaping brought by the root raised-cosine filter (RRCF), the passband bandwidth of the wavelength selective switch (WSS) is set as 42 GHz to filter the test channel. At the receiver (Rx) side, the filtered signal is beaten with the local oscillator (LO) in the integrated coherent receiver (ICR) with the 18-GHz bandwidth. Then, four balanced photo-detectors are adopted to carry out photo-electric detection. Finally, the baseband electric signals are captured by the 160-GSa/s real-time digital oscilloscope for offline DSP processing.

The block diagram of the DSP algorithms employed at the Tx and Rx is displayed in Fig. 3. As for the Tx DSP, the origin pseudo-random binary sequence (PRBS) is mapped into PS-64QAM signals by the constant composition distribution matcher (CCDM). The symbol pattern of the PS-64QAM signals is set as 20,480, with a pilot symbol being inserted in every 20 symbols for updating the weights of the equalizer. Here, pilot symbols will not be utilized for MAP-DDCPE to ensure fairness when compared with the blind phase estimation algorithm. Furthermore, the probability distribution of the generated PS symbols follows the power-efficient Maxwell–Boltzmann distribution. The detailed probability distribution of the PS-64QAM with the 5.2, 5.6, and 5.9 bits/symbol entropy is demonstrated in Fig. 1(b). The occurrence probability of the peripheral constellation points is significantly reduced with the increase of the shaping depth.

After that, a 128-tap RRCF with a 0.1 roll-off factor is adopted to realize frequency shaping. Finally, the 40-GBaud baseband signals are resampled to the sampling rate of the AWG. At the Rx side, the captured PDM signals at the test channel are first processed by the previous frequency offset estimation (Pre-FOE) based on the fast Fourier transform (FFT). Then, the $X$- and $Y$-polarization symbols undergo the Gram–Schmidt orthogonalization procedure (GSOP) and the retiming procedure based on the square timing algorithm, which eliminates the distortion induced by I/Q rotation and sampling deviation, respectively. The pre-processed symbols are then resampled to 1 Sa/symbol.

As for equalization, the adopted widely linear equalizer (WLE), introducing augmented complex analysis, outperforms the common linear equalizer due to its robustness against I/Q skew and imbalance^[19]. The taps of the WLE are optimized to 171 to compensate for the impairments. The weight coefficients of the MIMO-WLE are updated by the pilots to track the channel response, which follows the least mean square (LMS) algorithm. After that, the MAP-DDCPE is adopted to compensate for the phase noise. Given that the linewidth of the employed ECLs slightly fluctuates in the C-Band, the step-size factor of the MAP-DDCPE was optimized within the range of 0.0005 to 0.001. After the MAP-DDCPE, a 71-tap $4\times 4$ real-valued MIMO direct-detection LMS (DDLMS) equalizer is adopted to compensate for the crosstalk induced by the I/Q rotation and residual linear impairments before the final normalized generalized mutual information (NGMI) calculation. Finally, given that the NGMI exhibits great universality in measuring the performance of the PS signals with different modulation formats, the NGMI of the recovered signal is evaluated^[20].

To investigate the advantage of the adopted NANF, the NGMI curves of the PS-64QAM-5.9 signal after the 2-km NANF and SSMF transmission versus the launch power are demonstrated in Fig. 4. The NGMI performance of the PS-64QAM-5.9 signal after NANF transmission can be maintained even with an injected power of up to 23 dBm. In contrast, the NGMI performance of the signal after SSMF transmission degrades when the launch power exceeds 17 dBm. This indicates that the NANF exhibits great tolerance for high injected power due to its inherently low nonlinear effect. The recovered constellation diagrams of the single-channel signal after the 2-km NANF and SSMF transmission are also depicted in Fig. 4. The advantage of low nonlinearity in the NANF will become more pronounced with the increasing transmission distance, making it a crucial prospective solution for long-haul WDM transmission in the future. As for the WDM transmission over the NANF, we evaluate the NGMI performance of the signal at the ITU-T C30 channel versus the launch power. For this selected channel, the NGMI performance satisfies the SD-FEC threshold when the total launch power reaches 19.7 dBm.

Furthermore, we compare the NGMI performance of the PS-64QAM-5.2, PS-64QAM-5.6, and PS-64QAM-5.9 signals at 1550 nm with the proposed MAP-DDCPE, MPD-BPS, and PCPE after 2-km NANF transmission to investigate the PS-optimal CPE algorithms, which are depicted in Figs. 5(a)–5(c). Here, the performance of these CPE algorithms is investigated comprehensively in the shallow-shaping, moderate-shaping, and strong-shaping cases. The window length of the PCPE is set as 64, which is optimized for the NGMI performance. The window length of the MPD-BPS, ranging from 150 to 300, has also been optimized for different optical signal to noise ratio (OSNR) scenarios. The number of the searching stage in the MPD-BPS is set as 64. In the shallow- and moderate-shaping cases, the performance of the MPD-BPS and the PCPE shows limited performance compared to the MAP-DDCPE. Considering the 20% SD-FEC threshold, the MAP-DDCPE reduces the OSNR requirements by over 0.5, 0.7, and 1.8 dB compared to the other two CPE algorithms in the shallow-, moderate-, and strong-shaping cases, respectively. It is evident that the performance advantages of the MAP-DDCPE become more obvious with the increase in shaping depth. It is verified that the MAP-DDCPE is robust against the PS signals with various shaping depths and outperforms other CPE algorithms in the NANF transmission system. We believe that the proposed MAP-DDCPE is a promising PS-optimal CPE algorithm, which is suitable for broadband PS-assisted NANF transmission with varying entropy.

The NGMI performance of the 96-channel WDM PS-64QAM-5.9 signal, ranging from 191.45 to 196.2 THz at the C-band, is demonstrated in Fig. 6. As seen from the figure, the NGMI values of the 96 channels are mainly distributed in the range of 0.87 to 0.91, which are all above the 20% SD-FEC threshold. Meanwhile, the constellation diagrams of the $X$-polarization of signals at ITU-T C15, C30, and C45 are displayed in Fig. 6. The 96-channel transmission of the 40-GBaud PDM PS-64QAM-5.9 signal over the 2-km NANF has been successfully achieved. Considering the cost of the CCDM, the SD-FEC, and the pilots, the line rate approaches 96 channels × 2 polarizations × 40 GBaud × 5.9 bits/symbol/(1 + 20%)/(1 + 3.8‰)/(1 + 5%) = 35.82 Tbit/s.

To evaluate the calculation complexity, the number of real-valued numerical operations required for implementing the aforementioned CPE algorithms is listed in Table 1. Each complex-valued multiplication can be decomposed into four real-valued multiplications and two real-valued additions, respectively. Therefore, the multiplication between a complex matrix sized $m\times n$ and another complex matrix sized $n\times p$ requires $4m\times n\times p$ multiplications and $2m\times (n-1)\times p$ additions. Note that the $\arctan (·)$, $\exp (·)$, and $\ln (·)$ functions are all realized by the look-up table without the extra multiplication and addition.

As for the PCPE with the time window consisting of $N_{\mathrm{PCPE}}$ symbols, the calculation of the covariance matrix and the normalized principal component require $6N_{\mathrm{PCPE}}+7$ multiplications and $4N_{\mathrm{PCPE}}-1$ additions. After that, the phase estimation and unwrapping require more 4 multiplications and 4 additions. Lastly, $4N_{\mathrm{PCPE}}$ multiplications and $2N_{\mathrm{PCPE}}$ additions are required for the phase compensation. Given that the $N_{\mathrm{PCPE}}$ symbols within the time window share the same estimated phase, the total number of multiplications and additions required per symbol in the PCPE is $10+11/N_{\mathrm{PCPE}}$ and $6+3/N_{\mathrm{PCPE}}$. According to Ref. [18], $12N_{\mathrm{BPS}}$ multiplications and $22N_{\mathrm{BPS}}-1$ additions are required for each test phase. We suppose the number of the test phase is $B$. Given that the phase unwrapping and compensation requires 6 multiplications and 5 additions, the total number of multiplications and additions required per symbol in the MPD-BPS is $12N_{\mathrm{BPS}}B+6$ and $(22N_{\mathrm{BPS}}-1)B+5$. When it comes to the single-tap MAP-DDCPE, the phase compensation of the received symbol requires 4 multiplications and 2 additions. Furthermore, the MAP detection requires 5 multiplications and additions to obtain the decision error. After detection, 5 multiplications and 3 additions are required to update the estimated phase. It can be seen that the total number of multiplications and additions required per symbol in MAP-DDCPE is 14 and 10. The calculation complexity of the MAP-DDCPE and the PCPE is significantly lower than the MPD-BPS, which is more favorable for hardware implementation. However, the feedback structure of the MAP-DDCPE makes it difficult to parallelize. The parallel real-time implementation of the proposed MAP-DDCPE in the coherent system will be our future research orientation.

In this Letter, we have proposed a novel probability-aware CPE algorithm based on MAP detection and recursive decision-directed phase tracking, which enables PS-assisted broadband NANF transmission. The MAP-DDCPE cuts the OSNR requirement by more than 0.5, 0.7, and 1.8 dB with much lower calculation complexity in the shallow-, moderate-, and strong-shaping cases compared to the PCPE and the MPD-BPS. With the PS technology and the PS-optimal MAP-DDCPE, the remarkable 96-channel transmission delivering 40-GBaud PDM PS-64QAM-5.9 signals over the 2-km NANF is successfully demonstrated. We believe that the combination of the PS technology and PS-optimal CPE algorithm is a promising solution for the next-generation ultrahigh-capacity NANF transmission.