Guo-Qing Qin, Min Wang, Jing-Wei Wen, Dong Ruan, Gui-Lu Long, "Brillouin cavity optomechanics sensing with enhanced dynamical backaction," Photonics Res. 7, 1440 (2019)
Search by keywords or author
- Photonics Research
- Vol. 7, Issue 12, 1440 (2019)

Fig. 1. (a) Schematic of a Brillouin interaction in the parity-time symmetric system. The modes a 2 a 3 b a 1
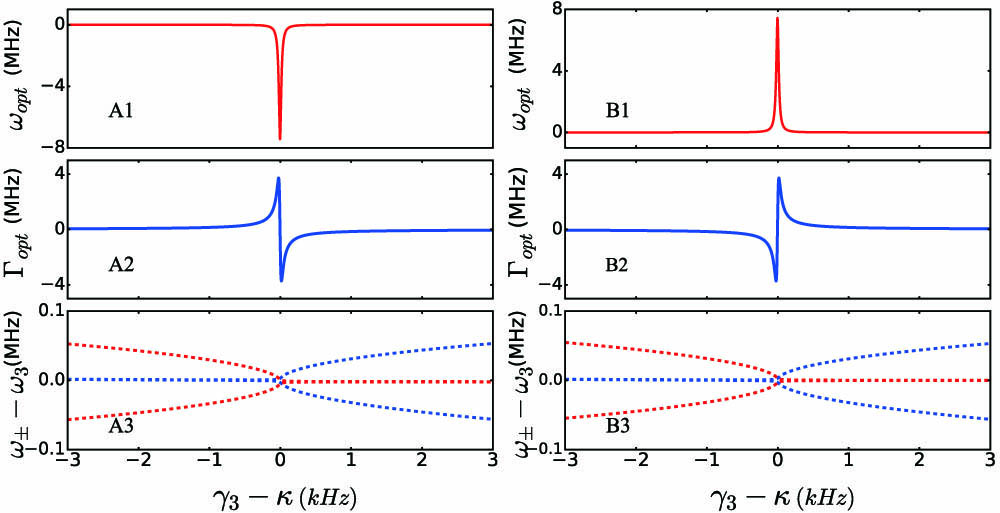
Fig. 2. Mechanical responses and the supermodes spectrum as a function of γ 3 Γ opt ω ± κ = 1 MHz P in = 17.5 μ W γ 2 = 2.6 MHz g 0 = 4 Hz Ω m = 50 MHz Γ m = 1 kHz J = κ δ 3 = − 1.95 kHz δ 1 = 0.99 δ 3
Fig. 3. Absolute value of the mechanical frequency shift Δ Ω m ( ν ) Γ ( ν ) ν Γ ( ν ) δ 1 = δ 3 = 5 kHz A b s ( Δ Ω m ( ν ) ) Γ ν δ 3 ν J 0.97 κ 1.01 κ γ 3 = 1 MHz κ = 0.975 γ 3 Γ = 5 Hz
Fig. 4. Cavity emission spectrum with the effect of laser frequency noise in (a) and (b). The perturbation ν σ J = 0.8 κ J = κ η σ J γ 3 = 1.00 MHz Δ 1 = Ω m Δ 3 = Ω m κ = 0.985 γ 3 Γ = 1 Hz
Fig. 5. (a) Normalized output spectra with different optical frequency shifts ν ν J Γ = 2 γ 3 = 1.00 MHz Δ 1 = Ω m Δ 3 = Ω m κ = 0.985 γ 3 J = κ

Set citation alerts for the article
Please enter your email address



