Mansour Bacha, Abderrahmane Belghoraf, "Numerical evaluation of radiation and optical coupling occurring in optical coupler," Chin. Opt. Lett. 15, 021301 (2017)
- Chinese Optics Letters
- Vol. 15, Issue 2, 021301 (2017)
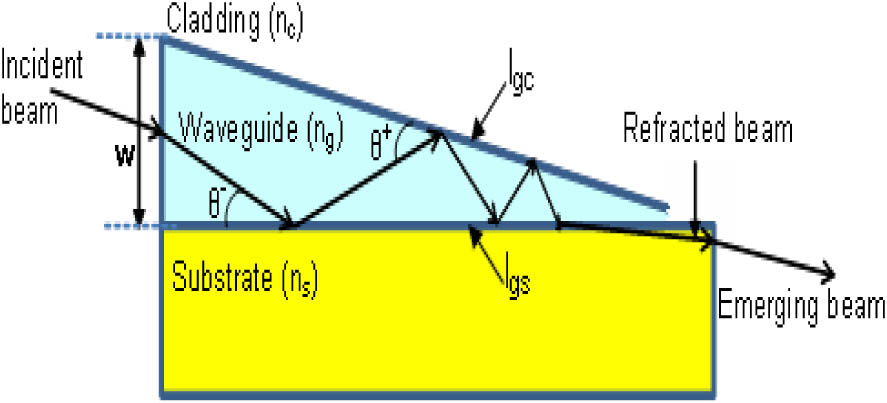
Fig. 1. Configuration of the optical coupler to analyze.
Fig. 2. Second intrinsic normalized mode (q = 2 a = 0.03 rad W = 3 μm W = 0.4
Fig. 3. Third intrinsic normalized mode (q = 3 a = 0.03 rad W = 4 μm W = 0.9
Fig. 4. Power distribution in the three regions of a symmetric tapered waveguide for the mode q = 3 a = 1 ° SiO 2 / Si / SiO 2
Fig. 5. Power distribution in the three regions of a symmetric tapered waveguide for the mode q = 3 a = 5 ° SiO 2 / Si / SiO 2
Set citation alerts for the article
Please enter your email address
© Copyright 2018-2021 | Chinese Laser Press. All Rights Reserved 沪ICP备15018463号-20