At present, laser interferometers serve as an effective way to detect the surface parameters of test mirrors according to the method of phase-step interferometry. For large-scale and long focal-length components, the demand for surface measurement requires a dynamic approach that is insensitive to vibrations. The mainstream dynamic measurement methods include simultaneous phase-shifting^[1–5] and single-frame images with spatial carrier phase-shifting methods^[6,7]. Simultaneous phase-shifting methods mainly involve completing the phase shift concurrently, and single-frame images can be collected, or multi-detector phase-shifting methods can be used, which may result in a loss of spatial resolution and inherent biases at different spatial positions, requiring algorithmic correction and calibration. The spatial carrier phase-shifting method used in single-frame phase-shifting is sensitive to displacement-induced errors and has limited spatial resolution, resulting in limited computational accuracy. Here, we utilize heterodyne phase-shifting technology to increase the phase-shifting frequency under the basic vibration conditions of laboratory components. This technique ensures effective vibration resistance while maintaining a high spatial resolution and a simple instrument configuration.

Heterodyne phase-shifting technology is widely used in displacement and velocity measurements^[8], with interferometric applications in surface measurement mostly used in low-frequency testing^[9–12]. There are still few attempts to increase the heterodyne frequency and apply this method in vibration environments to measure surface parameters. Additionally, heterodyne phase shifting offers greater flexibility regarding phase shift steps and algorithms. Changing the phase shift frequency and detector sampling frequency makes optimizing the measurement steps easier to adapt to different measurement environments^[13,14]. For example, a low beat frequency with multi-step phase shifting on stable tables can be selected to achieve a higher measurement accuracy^[15–17]. In environments with ambient random vibrations, high-frequency low-step phase shifting can enhance anti-vibration performance, allowing rapid acquisition of object surface parameters and wavefront information while maintaining great spatial resolution and stable repeatability^[18]. As light source energy and detector performance improve, full-field heterodyne long-arm measurement technology is expected to evolve towards transient measurements^[19,20]. It may become a future research trend in high-precision interferometric measurements resistant to vibrations. Therefore, it is important to study methods of heterodyne long-arm interferometry.

In this Letter, we studied the surface measured method of high-frequency full-field heterodyne long-arm interferometry. We introduced the basis of the theory and the components of the method. Basic measurements are performed on the vibration of general laboratory components, and the measurement results are substituted into the interference model to simulate the impact of vibration on measurement error and repeatability. Finally, for the test of a surface 22 m away, we use different beat frequencies to verify this technique’s vibration suppression capability and root mean square (RMS) repeatability. This interferometry does not require complex components and optical path designs. Under general laboratory conditions for long-distance measurements, the measurement repeatability is better than 0.8‰ wave RMS at 633 nm, which shows great anti-vibration performance and measurement robustness.

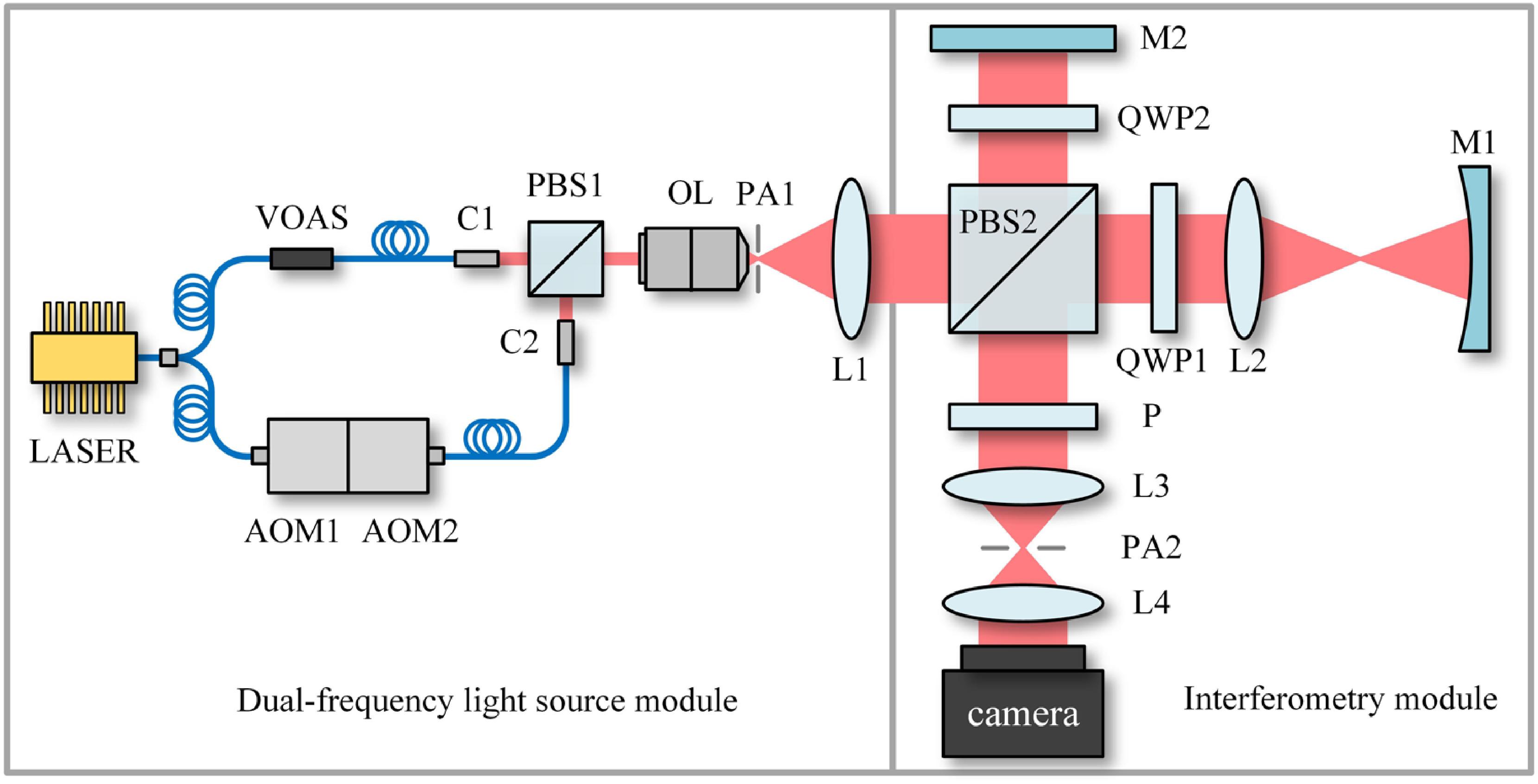
The schematic diagram of the full-field heterodyne long-arm interferometry is shown in Fig. 1. The overall structure consists of a dual-frequency light source module and a Twyman–Green measurement module.

The main purpose of the dual-frequency light source module is to obtain orthogonally polarized beat frequency laser signals at 633 nm. Using our self-developed light source drive and temperature control circuit, we can maintain the coherence length of the light source at over 100 m. The temperature variation range of the light source is controlled within $\text{(}25\pm 3\text{)}°\mathrm{C}$, with a corresponding temperature control accuracy of 10 mK. The light is split into two paths through a fiber splitter, specifically divided into paths A and B. Path A is coupled through an electrically controlled variable optical attenuator (VOA) to fiber collimator 1 (C1), which outputs spatial light. The VOA can adjust the energy intensity of the light in path A to change the split ratio of the two light paths. Due to the energy adjustment between the two paths, the interferometer is capable of precision surface tests of different reflectivities. Path B employs two coupled fiber acousto-optic modulators (AOM1 and AOM2). Using different diffraction orders of the AOMs to produce a precise frequency shift related to path A, we can avoid the production of excessive high-frequency shifts by a single AOM. AOMs are coupled to centrally handle the additional diffraction and harmonic errors introduced by the AOMs. This configuration allows for efficient adjustment of the splitting ratio between the optical paths, ensuring high energy efficiency and optimal utilization. The designed frequency AOMs module can produce an accurate frequency shift of 800 Hz. Additionally, the harmonic noise of the driver module remains within $-80\mathrm{dB}$. The frequency signals from paths A and B output as spatial light and then pass through fiber collimators C1 and C2. The polarization beam splitter (PBS1) affects the polarization state of the spatial light, ultimately obtaining orthogonally polarized dual-frequency linear light output. Through mechanical control, the coupling point center of the two light paths at a distance of 1 m has a spot center offset of $<10\mathrm{\mu m}$, i.e., the spatial angular deviation of the two light paths is within ${0.07}^{\prime }$, which effectively controls the offset of the synthetic dual-frequency lights on the propagation errors of the interferometer. The synthetic lights are then converged by an object lens (OL) at the convergence point, where a 10 µm pin aperture (PA1) is placed to obtain a well-conditioned spherical wavefront without too much energy loss. The spherical wave is collimated by lens 1 (L1) and then enters the Twyman–Green interference module.

The interferometry module mainly consists of a Twyman–Green interference part and a camera, which is primarily responsible for generating interference fringes and processing measurement data. PBS2 separates the collimated synthetic dual-frequency lights. Aligning PBS2 with PBS1 so that the lights of different frequencies in paths A and B are separated, the light in path A passes through PBS2, a quarter-wave plate 1 (QWP1), and divergent lens 2 (L2) to obtain a converging spherical wave. The spherical wave then travels a long distance to the mirror under test (M1) and is reflected by the mirror along the same path to PBS2. Due to passing through the QWP twice, the polarization direction of the light is perpendicular to the original direction, and the PBS2 reflects the light to reach the polarizer. Similarly, the beam splitter of PBS2 reflects the beam in path B and then passes through the QWP2 to the reference surface (M2). The light reflected by M2 returns along the same path to PBS2. Similarly, as it passes through the QWP2 twice, the polarization direction of the light in path B changes, and the light passes through the PBS2 to reach the polarizer. Both lights ultimately reach the detector through the imaging system (L3 and L4), where the detector records the interference information of both lights and transmits it to the upper computer to obtain the corresponding measurement results. The aperture stop PA2 serves as the imaging aperture stop.

The main factors affecting the measurement accuracy of this interferometer are the offset and the leakage of synthetic dual-frequency lights. Using a PBS with a high extinction ratio and controlling the relative angle between the two PBSs in ${30}^{\prime }$, we can ensure that the leakage ratio of the light beams to the test mirror surface is better than 0.03. This setup can reduce the impact of mixing frequencies on the measurement results to less than 0.001 waves^[21].

Due to the frequency shift of the two lights, the intensity distribution of the light with the beat frequency on the detector is $$I(x,y,t)=I_1(x,y)+I_2(x,y)\cos [2\pi \mathrm{\Delta }ft+\mathrm{\Delta }\phi (x,y)],$$(1)where $I_1(x,y)$ is the background light intensity at the detector, $I_2(x,y)$ is the modulated light intensity, $\mathrm{\Delta }f$ is the frequency difference between the two lights, which is the beat frequency, $\mathrm{\Delta }\phi (x,y)$ is the phase of the light, and $t$ is the sampling moment of the detector. The relatively accurate four-step phase-shifting results can be ensured by controlling the sampling frequency $\nu$ to be four times the beat frequency $\mathrm{\Delta }f$, $$\{\begin{array}{c}I(t_1)=I_1+I_2\cos [2\pi \mathrm{\Delta }f(t_0+1/\nu )+\mathrm{\Delta }\phi ]\\ I(t_2)=I_1+I_2\cos [2\pi \mathrm{\Delta }f(t_0+2/\nu )+\mathrm{\Delta }\phi ]\\ I(t_3)=I_1+I_2\cos [2\pi \mathrm{\Delta }f(t_0+3/\nu )+\mathrm{\Delta }\phi ]\\ I(t_4)=I_1+I_2\cos [2\pi \mathrm{\Delta }f(t_0+4/\nu )+\mathrm{\Delta }\phi ]\end{array}.$$(2)

For long-distance measurements, it is difficult to place the M1 and the interferometer on the same vibration isolation optical table. Vibrations will introduce significant errors in surface measurement.

Figure 2 shows the results of the vibration measurements of the laboratory ground. The measurement is carried out using a piezoelectric accelerometer. Figure 2(a) shows three measurements at the same location in the laboratory, while Fig. 2(b) shows measurements at three different locations in the laboratory. The vibration amplitude is expressed logarithmically in nanometers (nm), and the displayed frequency is determined based on the frequency corresponding to the vibration criteria^[22]. This illustrates that low-frequency errors around 0–100 Hz can be introduced on non-vibration-isolated optical tables. It confirms that the current laboratory amplitude level of vibration at 0–10 Hz is below 0.5 waves. At 10–50 Hz, it is below 0.05 waves, and at 50–100 Hz, it is below 0.005 waves.

Figure 3 is a schematic diagram of the vibration measurement of the lens on the small optical table. The measurement was carried out using a triaxial seat pad piezoelectric accelerometer. The measurement results are shown in Fig. 4. Figures 4(a)–4(d) show the vibration frequencies and amplitudes in the $X$-, $Y$-, $Z$-directions and the composition direction, respectively. The vibration amplitude is expressed logarithmically in nanometers, and the displayed frequency is measured based on the range of 0–100 Hz. It can be found that even on an ordinary optical vibration isolation table, the higher amplitude levels within the three vibration frequency bands of 0–10, 10–50, and 50–100 Hz are still within the previously divided amplitude range. Therefore, the subsequent lens vibration is simulated mainly according to these three frequency bands and their corresponding amplitude levels.

Simulations were conducted on sampling test points with sinusoidal vibrations introduced at 10, 50, and 100 Hz frequencies and their corresponding amplitudes. The results are shown in Fig. 5.

The ideal light intensity variation curve is shown in blue, while the curve that introduces three vibration frequencies is shown in red. The frequency and amplitude of the introduced vibrations are selected based on the three vibration bands identified in previous experimental measurements, which are 1 waves at 10 Hz, 0.1 waves at 50 Hz, and 0.01 waves at 100 Hz. The optical path difference (OPD) of the introduced vibration is twice as much as the amplitude, which is 1 wave at 10 Hz, 0.1 waves at 50 Hz, and 0.01 waves at 100 Hz. The yellow curve represents the sampling light intensity results corresponding to the random vibration frequency, the amplitude, and the initial phase information of $0–1\lambda$, $0–0.1\lambda$, and 0–0.01 in the three vibration bands of 0–10, 10–50, and 50–100 Hz. There are ten random vibration errors in each vibration band, for a total of 30 random vibration sampling errors. The four graphs represent the beat frequency at 5, 50, 400, and 800 Hz. Although the 5 Hz sampling points coincide with the ideal sampling points, this is only true for results under the vibration frequencies of 10, 50, and 100 Hz. The actual vibration conditions can be much more complex. Thus, 5 Hz sampling cannot satisfy the requirements for other types of vibration frequencies.

Vibration-induced errors in interferometry can be described as $$I(x,y,t)=I_1+I_2\cos [2\pi \mathrm{\Delta }ft+\mathrm{\Delta }\phi (x,y)+\delta \phi (t)].$$(3)

Here $\delta \phi (t)$ represents the measurement phase change introduced by actual vibration information.

With the $K$ phase shifting discrete sampling function, it is given by $$\tan \phi =-\frac{\sum _{k=1}^K{I}_k\sin {\phi }_k}{\sum _{k=1}^K{I}_k\cos {\phi }_k}=\frac{A}{B},{\phi }_k=2\pi \mathrm{\Delta }f{t}_k,t_k=\frac{k-1}{K\mathrm{\Delta }f}.$$(4)

Here $t_k$ is the sampling time of the intensity of the beat light at $k$-step phase shifting. The corresponding phase error is $$\delta \phi =\phi -\mathrm{\Delta }\phi =\arctan \left\{\frac{\sum _{k=1}^K\cos [2\pi \mathrm{\Delta }f{t}_k+\mathrm{\Delta }\phi +\delta \phi \left(t_k\right)]\sin (\mathrm{\Delta }\phi +2\pi \mathrm{\Delta }f{t}_k)}{\sum _{k=1}^K\cos [2\pi \mathrm{\Delta }f{t}_k+\mathrm{\Delta }\phi +\delta \phi \left(t_k\right)]\cos (\mathrm{\Delta }\phi +2\pi \mathrm{\Delta }f{t}_k)}\right\}.$$(5)

Figure 6(a) illustrates the phase errors of different beat frequencies under the previous statement vibration condition. It shows that increasing the beat frequency effectively reduces the measurement error. A beat frequency above 500 Hz can ensure that the total phase error introduced by a single cycle of vibration within 100 Hz is below $0.1\pi$.

Figure 6(b) shows the measurement error at two points with different beat frequencies under the introduced vibration states mentioned before. Without loss of generality, we set the height of the points at 0.1 waves, as the phase of the OPD is close to $0.5\pi$. Therefore, the calculation value is close to a sine function cycle. It shows that the phase error introduced at beat frequencies above 1500 Hz is better than 0.005 waves. The measurement error simulated is better than 0.01 waves with a beat frequency above 750 Hz. A beat frequency of 800 Hz in the laboratory can hold the measurement accuracy errors under vibration conditions within 0.01 waves.

With beat frequencies of 5, 10, 40, 100, 200, 400, and 800 Hz, multiple tests were conducted on a 200 mm aperture mirror located 22 m away, on a different vibration-isolated optical table in a laboratory environment with various levels of vibration. The measurement setup is displayed in Fig. 7(a). The phase-shifting interferograms and the measurement results are displayed in Fig. 7(b).

Single vibration frequency may introduce various special influences on some beat frequencies. We simulate the RMS repeatability for 10,000 random measurements under three frequency bands of random vibrations at 1–10, 20–50, and 50–120 Hz.

Figure 8 shows the simulation and measurement results of the RMS repeatability. The red lines correspond to the RMS repeatability error results for random vibration amplitude, frequency, and phase for the three selected frequency bands. The light red sections correspond to the confidence intervals for the simulated data fluctuations. The measurement of RMS repeatability refers to the definition of result $1\sigma$ from the RMS values of the surface form results from 10 sets of measurements, each set being the average of 16 measurements^[1].

When the beat frequency selection is below 200 Hz, the induced vibration frequency has a significant error impact on the repeatability results. Hence, a larger range of fluctuation in the standard deviation. When the beat frequency is above 200 Hz, due to the higher sampled beat frequency relative to the random vibration frequencies, the sampling time has a suppressive effect on the vibrations, and as the sampling frequency increases, the fluctuation range of the standard deviation for the measurement repeatability simulation results of multiple groups gradually decreases, approaching alignment with the average line.

The blue line represents the repeatability results of experiments conducted on a test mirror 22 m away with different beat frequencies. It can be observed that the impact of vibrations on the repeatability of actual experimental measurements gradually decreases at sampling frequencies above 200 Hz. In practical experiments, the impact of vibrations is significantly less than that of other factors (frequency aliasing, acoustic noise, airflow noise, and light source intensity noise). The repeatability data in the 20 m experimental environment remain below 0.8‰ wave RMS. It is important to note that although the impact of vibrations on repeatability is small under a 200 Hz beat frequency, actual vibrations are more complex than the ideal three vibration bands. Due to the air turbulence, stray light, and other factors, the actual RMS repeatability is higher than the simulated theoretical value curve.

Therefore, by increasing the sampling frequency, it is possible to effectively suppress the impact of vibrations and other factors on the repeatability of the surface form measurements at long distances. As the detector performs better, an appropriate frequency can be selected to employ different step phase-shifting algorithms for various testing scenarios.

In summary, a high-frequency full-field heterodyne interference method is presented for measuring mirrors at long distances, which aims at suppressing vibrations. For measurements of mirrors at long distances, the repeatability of this technique is better than 0.8‰ wave RMS with 800 Hz beat frequency. This demonstrates that this method can effectively reduce the impact of vibrations on measurement results in most laboratory environments. Similarly, heterodyne phase shifting combined with low-coherence light sources can be applied to Fizeau interferometric measurements. As detector performance improves in the future, the high-frequency full-field heterodyne interferometry measurement technology may be applied to more measurement interferometers to achieve better measurement precision and RMS repeatability in long-distance vibration detection environments. It offers an effective method for high precision and performance surface form interferometry and is likely to become a trend in developing anti-vibration precision interferometric measurements. Moreover, improvements in heterodyne interferometry are already underway.