The phase modulator is one of the most indispensable devices in the optical field that is used to control the phase of light by an external signal, and it has important applications in laser, sensing, and quantum^[1–3]. To enable better compatibility of devices with the typical fiber-optic systems, all-fiber phase modulators with low cost and low insertion loss have been widely studied by researchers. At present, the schemes based on all-fiber phase modulation mainly include electro-optical modulation^[4] and all-optical modulation^[5]. Compared with the former, the latter has the advantages of low transmission loss, large operating bandwidth as well as fast response speed^[6]. Moreover, benefiting from the high photo-thermal coefficients of two-dimensional (2D) materials, such as graphene^[7–9], MXene^[10,11], and tungsten disulfide (${\mathrm{WS}}_2$)^[12,13], the combination of 2D materials and microfibers makes all-optical phase modulation possible. In the above schemes, the 2D materials are typically deposited on the surface of a microfiber, and then phase and intensity modulation of the optical signal can be achieved via further integration with a fiber Michelson interferometer (MI) and a Mach–Zehnder interferometer (MZI). However, the MZIs and MIs with large volumes are not conducive to device integration, and they are extremely sensitive to external interference, which tends to make the phase shift of the device uncontrollable. Despite the small size of the microfiber knot resonator (MKR), it has long-term stability, and its complexity in fabrication and the fragility of the microfibers bring inconvenience to the MKR-based modulators in practical applications^[10].

Because of its simple fabrication and stability, fiber in-line interferometers are widely applied in the fields of fiber sensors and optical filters^[13–15]. Similarly, it also provides an excellent platform for all-optical modulation. Chu et al. reported an all-optical phase shifter based on graphene and a twin-core fiber MI and achieved an optical switching with a response time of 55.8 ms^[16]. Yi et al. proposed an all-optical phase modulator by combining MXene with a compact in-line MZI and greatly improved the sensitivity of the phase modulator using polydimethylsiloxane^[17]. However, the 2D materials need to be deposited on the surface of the fiber in the above schemes. Thus, not only does the fabrication of the device require a complex process but the materials located on the surface of the fiber are susceptible to external pollution, which means the device in practical applications will face the challenge of maintaining long-term environmental stability. For comparison, the fiber doped with rare-earth ions has a high photo-thermal coefficient and good environmental stability^[18]. In previous research, we achieved all-optical phase modulation by combining Er/Yb co-doped fiber (EYDF) and in-line Fabry–Perot interferometer (FPI), and the proposed device is simple to fabricate, compact, and has long-term environmental stability. However, limited by the thermal response of the EYDF, the modulation speed of the device is relatively slow ($\sim 221\mathrm{ms}$)^[19].

In this Letter, we propose a scheme to achieve all-optical phase modulation using a compact fiber in-line FPI platform as well as the nonlinear and thermo-optic effects in EYDF. Compared with Ref. [19], the proposed device is further improved in its structure, in which the reflective FPI is fabricated by splicing the hollow-core fiber (HCF) and EYDF. In particular, the EYDF is set as an F-P cavity, which not only greatly improves the sensitivity of the phase modulation, but also introduces a nonlinear phase shift to the F-P cavity, enabling the device to achieve all-optical phase modulation at a high frequency. This scheme has the advantages of compact structure, simple fabrication, and good stability, providing an avenue to all-optical phase modulation in all-fiber systems.

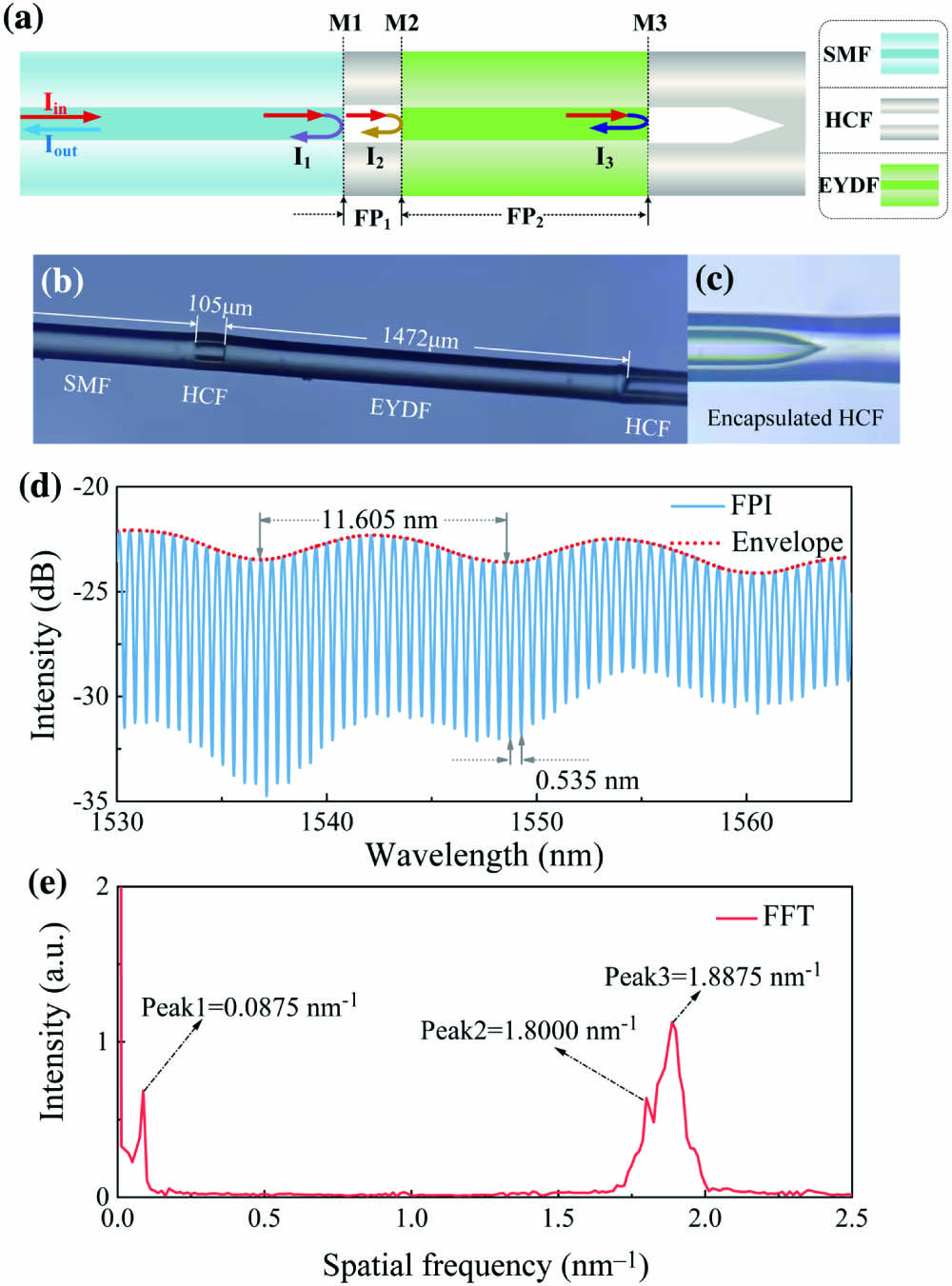
The schematic diagram of the EYDF-based reflective FPI is shown in Fig. 1(a). The FPI of the all-fiber structure is made by splicing commercial fibers using a fusion splicer (FSM-45PM, Fujikura) and a fiber cleaver. To enable the EYDF so that it can be used as an F-P cavity, we add a short HCF at the front of the EYDF to form a reflective surface for the EYDF, which is fabricated as follows. First, the input single-mode fiber (SMF) is fused to a short HCF using a fusion splicer, which creates a mirror surface (M1) at the splice because the refractive index (RI) of the SMF core is greater than that of the HCF core (air). Subsequently, a section of EYDF is fused to the SMF-HCF cascade structure, also due to the difference in the RI between the EYDF core and the air, and two mirror surfaces are formed at the ends of the EYDF, namely M2 and M3. Finally, the FPI is encapsulated using a section of the HCF. As shown in Fig. 1(c), a tapered structure is formed at the end of the HCF by discharging to prevent M3 from being polluted from the external environment. Figure 1(b) illustrates the micrographs of the fabricated FPI, where the lengths of the HCF and the EYDF are 105 µm and 1472 µm, respectively.

The whole FPI has two F-P cavities, and the reflected spectrum is produced by three-beam optical interference. The reflected light of the FPI can be written as $$\begin{gathered} I_{\mathrm{out}}=I_1+I_2+I_3+2\sqrt{I_1{I}_2}\cos ({\varphi }_1) \\ +2\sqrt{I_2{I}_3}\cos ({\varphi }_2)+2\sqrt{I_1{I}_3}\cos ({\varphi }_3), \end{gathered}$$(1)where $I_1$, $I_2$, and $I_3$ represent reflected light at M1, M2, and M3, respectively. The phase differences caused by the air cavity (${\mathrm{FP}}_1$), the silica cavity (${\mathrm{FP}}_2$), and the mixing cavity are ${\varphi }_1=(4\pi L_1{n}_{\mathrm{air}})/\lambda$, ${\varphi }_2=(4\pi L_2{n}_{\mathrm{EYDF}})/\lambda$, and ${\varphi }_3={\varphi }_1+{\varphi }_2$, respectively. Figure 1(d) shows the measured reflected spectrum. By comparison with the light source spectrum, the transmission loss of the FPI is obtained to be about 10 dB. The entire spectrum of the FPI is a periodic interference fringe, and its free spectral range (FSR) is 0.535 nm. In addition, a distinct spectral envelope can be seen in the reflected spectrum, as shown by the dotted curve in Fig. 1(d), which has an FSR of 11.605 nm. By performing the fast Fourier transform (FFT) function on the reflected spectrum of the FPI, its corresponding spatial frequency spectrum is obtained, as shown in Fig. 1(e). There are three main frequency peaks. Peak 1 has a spatial frequency value of $f_1=0.0875{\mathrm{nm}}^{-1}$, which is caused by air cavity interference. The spatial frequency value of Peak 2 is $f_2=1.8000{\mathrm{nm}}^{-1}$, which is caused by the interference of ${\mathrm{FP}}_2$ with a large cavity length. Peak 3 is caused by the mixed cavity and corresponds to a spatial frequency value of $f_3=f_1+f_2=1.8875{\mathrm{nm}}^{-1}$. Furthermore, the relationship between the spatial frequency value and the cavity length can be expressed as $f=2nL/{\lambda }^2$. Therefore, the lengths of the air and silica cavities can be calculated as 105.5 µm and 1480 µm according to $f_1$ and $f_2$, which are in good agreement with the experimental measurements. Note that here we use the EYDF as the silica cavity, and the rare-earth ions in the EYDF can generate a lot of heat after absorbing the optical pump. For a silica cavity, when the external temperature changes, its RI will change accordingly via the thermo-optic effect, which also makes the phase of the optical signal transmitted in the cavity shift. The phase shift induced by temperature is described as $$\mathrm{\Delta }\varphi =\frac{4\pi \delta L_2}{\lambda }\mathrm{\Delta }T,$$(2)where $\delta =\mathrm{d}n/\mathrm{d}T=1.1\times {10}^{-5}{\mathrm{K}}^{-1}$ is the thermo-optic coefficient of the silica. Therefore, the phase shift can be flexibly regulated by adjusting the power of the optical pump in the experiment. In contrast, since the air cavity has a lower thermal-optical coefficient, the phase change due to temperature is not significant, which can be observed later in the experiments, and therefore we neglect it here.

Figure 2(a) shows the experimental setup diagram for the dynamic phase tuning of the EYDF-based FPI. The input light comes from a broadband light source (BLS) or tunable laser source (TLS), in which the BLS is used to measure the reflected spectrum of the FPI, and the TLS is used to measure the modulation response. To dynamically tune the phase shift in the FPI, a laser with a central wavelength of 973 nm and controllable optical power is used for the pump, which passes through the wavelength division multiplexer (WDM) along with the signal light and then enters the FPI. Moreover, in order to measure the response speed of the device during the modulation process, the pump light is modulated into a pulse sequence by the electro-optic modulator (EOM) and the arbitrary waveform generator (AWG). Finally, the reflected light of the FPI is monitored by an optical spectrum analyzer (OSA, Anritsu CMA5000) or detected by a photodetector (PD) and a digital storage oscilloscope (DSO) after passing through the circulator (CIRC). Figure 2(b) is a photograph of the fabricated FPI excited by the pump light. The EYDF emits green fluorescence under the excitation of 973 nm optical pumping.

In the experiment, we first investigate the relationship between the FPI spectra and pump light by using BLS and OSA. Figure 3(a) gives the reflected spectra at different pump powers, where the solid lines are the interference fringes and the dotted lines are the envelopes of the interference spectra. Figure 3(b) shows the envelopes at different pump powers, and it can be seen that there is no significant wavelength shift in the envelopes with the increase of the pump power, indicating that the temperature change induced by the pump has minimal effect on the phase of the air cavity. However, the fine interference fringes shift to longer wavelengths with increasing pump power, and the maximum shift of the wavelength dip at a pump power of 120 mW is 1.005 nm, as shown in Fig. 3(c). As the pump light is switched off, the spectrum will also return to its initial position. During the modulation process, only the extinction ratio (ER) of the interference fringes has a change of 1.42 dB (from 11.27 dB at 0 mW to 9.85 dB at 120 mW), while there is no significant change in the FSR and the spectral lineshape, suggesting that the device has a good stability. According to the above theory, the interference spectrum shift is caused by the phase change in the EYDF. Thus, the corresponding phase change can be calculated from the shift of the wavelength dip, which can be expressed as $\mathrm{\Delta }\varphi =2\pi \mathrm{\Delta }\lambda /\mathrm{FSR}$. The phase shifts at different pump powers are shown in Fig. 3(d). Carrying out the linear fitting to the measured data, a phase modulation sensitivity of $0.0312\pi /\mathrm{mW}$ is obtained. The EYDF in the proposed structure acts as both a heater and a medium for the F-P cavity. Compared with our previous work, this “zero-distance” heating greatly reduces the heat loss and improves the sensitivity of phase modulation.

Subsequently, we explore the temporal response of the device during modulation. From Fig. 3(c), we know that the spectrum will red shift with increasing pump power. Therefore, when the input light is a narrow linewidth continuous wave (CW) and the center wavelength is located near the spectral dip, the center wavelength will move towards the spectral peak as the pump power increases, which results in the output light intensity of the FPI also being modulated by the pump light, from weak to strong. In the experiment, we set the output wavelength of the TLS to 1537.1300 nm, and the 973-nm pump is modulated into a periodic square wave. When the modulation frequency is 1 Hz, the CW signal is successfully modulated by the pump light into a pulsed light with a corresponding period, as shown in Fig. 4(a). The response time of the modulation is 204 ms, which is obtained by observing the time needed for the voltage to rise from 10% to 90%. This low-speed thermal modulation can be used in some applications that do not require high modulation speed, such as tunable optical filters.

Since the EYDF acts as a cavity for the FPI, the intensity change of the optical signal at 1 Hz is caused by the thermal phase shift of the thermo-optic effect and the nonlinear phase shift of the electronic effect. The generation of the nonlinear phase shift is due to the doped rare-earth ions showing a strong absorption band in the spectrum, while the input pump light will change the absorption of the rare-earth ions by partially depleting its ground state. Based on the Kramers–Kronig (K-K) causality, the RI of the fiber will change accordingly. Compared to the thermal phase shift, the nonlinear phase shift has a fast response speed, which depends on the substable lifetime of the rare-earth ions in the fiber. Therefore, the thermal phase shift will be averagely cancelled out at a high modulation frequency, leaving only the nonlinear phase shift^[20]. Figure 4(b) presents the output waveform at a modulation frequency of 100 Hz, where the continuous signal light is likewise modulated into a pulsed signal. The measured response speed of the modulation is 2.5 ms, which is 2 orders of magnitude faster than the thermal phase shift. However, the peak-to-peak voltage of its pulses is only about 2.5 mV, compared to 50 mV for a pulse at 1 Hz, indicating the phase change induced by thermo-optic and electronic effects is about 1:19.

To better illustrate the transition from thermal to nonlinear phase shift, the output signal waveforms at modulation frequencies of 5 Hz, 10 Hz, and 50 Hz are given in Fig. 5. It can be clearly seen that when the modulation frequency is increased from 1 Hz to 10 Hz, the signal waveform gradually changes from a square to a triangle due to the hysteresis of thermal conduction and diffusion, accompanied by a gradual decrease in the peak voltage. Note that the thermal-optic effect (i.e., thermal phase shift) is still dominant in this state, and its response time is independent of the modulation frequency, which depends mainly on the material and structural properties of the EYDF. As the modulation frequency is increased to 50 Hz, the output signal changes from a triangular wave to a square-like wave, the thermal phase shift decreases, and the nonlinear phase shift dominates. However, limited by the length of the EYDF and the concentration of the doped rare-earth ions (the peak cladding absorption coefficient at 915 nm is 3.03 dB/m), the modulation sensitivity of the nonlinear phase shift is still relatively low. In addition, as shown in Fig. 4(a), the presence of the thermal phase shift also results in a slow temporal response at a low modulation frequency. Indeed, further increasing the concentration of rare-earth ions in fiber can solve the above problems. For example, Janos et al. obtained nonlinear phase shift of $\pi$ in a 0.005-m length, highly doped Er/Yb fiber grating using a pump with a power of only 50 µW^[21]. Therefore, by increasing the concentration of the rare-earth ions in our scheme, not only is the modulation sensitivity of the nonlinear phase shift improved but also the low power pump avoids the thermal phase shift caused by the thermo-optic effect and hence improves the modulation speed at a low modulation frequency.

Table 1 summarizes the research state of the all-optical modulators with different structures and materials. It can be seen that the proposed modulators perform relatively well in terms of modulation sensitivity and temporal response. However, compared with modulation schemes based on MI or MZI, the proposed all-optical modulator is more compact and has the advantages of excellent stability^[5,12,16,22]. In addition, the modulator requires only a simple splicing of commercial fibers, which makes it simpler and more robust in construction than the MKR^[10]. In particular, the scheme does not require the 2D material to be coated on the surface of the fiber, leading to a good environmental stability of the proposed modulator.

To verify that the fabricated device has good environmental stability, we placed the encapsulated FPI in a mixture of water and glycerol with different concentrations. The RI of the mixed solutions is calibrated using an Abbe refractometer with a resolution of $\pm 0.0002$. Figure 6 shows the reflected spectra of the FPI at RIs from 1.3334 to 1.3706. It can be seen from the inset that there are no significant fluctuations in the reflected spectra, including shifts in wavelength dip and changes in the FSR and the ER. Thus, the proposed modulator has a strong resistance to external pollutions, such as dust and humidity, which will extend its usage scenario in practice.

In summary, we have presented an all-optical phase modulation scheme based on an EYDF and in-line FPI. The proposed device is an all-fiber structure, fabricated by splicing commercial fibers HCF and EYDF. Benefiting from the rational design of the EYDF as an F-P cavity, the modulator introduces both a nonlinear and a thermal phase shift. The maximum tunable phase shift is $3.76\pi$, with a phase sensitivity of $0.0312\pi /\mathrm{mW}$. Further improvement of the response speed at a low modulation frequency and modulation sensitivity may be achieved by using the EYDF with higher dopant concentrations in the device. We believe that this scheme has potential applications in optical filters, sensors, and optical communications.