High-security multi-constellation shaping modulation with asymmetric encryption

Lei Jiang; Bo Liu; Jianxin Ren; Xiangyu Wu; Rahat Ullah; Yaya Mao; Shuaidong Chen; Yilan Ma; Lilong Zhao; Feng Tian

doi:10.3788/COL202422.040602

Abstract

This Letter proposes a high-security modulation scheme for optical transmission systems. By using multi-constellation shaping and asymmetric encryption, the information security can be enhanced and quantum computer cracking can be effectively resisted. Three-dimensional (3D) carrier-less amplitude phase modulation is utilized to superposition and transmit 3D signals. Experimental verification is conducted using a seven-core weakly coupled fiber platform. The results demonstrate that the proposed scheme can effectively protect the system from any illegal attacker.

Keywords

asymmetric encryption multi-constellation shaping multi-core transmission

1. Introduction

Due to the popularity of new technologies such as 5G, artificial intelligence, cloud computing, and intelligent terminals, data are automatically generated and processed centrally. This greatly enhances people’s ability to use data and marks a transition from informatization to digitization. The digital age is following an unavoidable historical pattern. As the carrier of digital information, future communication networks will require higher capabilities and standards, particularly in terms of speed, capacity, and security. In recent years, space division multiplexing (SDM) optical transmission systems have developed rapidly^[1–5]. As a result, it is foreseeable that future optical communication systems will switch from the current single-core single-mode to multicore multimode designs. This upgrade is expected to increase system capacity several dozen times over. An SDM transmission system over a 10 km seven-core fiber capable of transmitting up to 560 Tbit/s was reported^[4]. This system uses a discrete Fourier transform to spread 32 quadrature amplitude modulation (QAM) orthogonal frequency-division multiplexing (OFDM) as the modulation format. Therefore, multicore optical transmission is the most likely to be commercialized in SDM systems.

The SDM optical communication system’s channel capacity has been dramatically enhanced due to the increase in physical channels, making it a more suitable candidate for the optical industry to grow. In traditional single-mode single-core optical transmission systems, the single channel and coding modulation dimensions are independent of each other. Future SDM optical communication systems possess inherent physical channels’ advantages and require further coding domain exploration. Several domestic and foreign research institutions and scholars have been investigating three-dimensional (3D) and even higher-dimensional encoding techniques^[6–10]. Although there is currently no industry-wide standard, this will be a crucial focus of communication system research in the future. A 3D probabilistically shaped carrier-less amplitude phase (CAP) modulation based on constellation design using regular tetrahedron cells was experimentally proved to improve the system’s performance^[8].

As the production, transmission, storage, and retrieval of vast amounts of information data become increasingly prevalent, information security becomes ever more important. Data security is related to individuals’ privacy and business, national security, and other larger concerns. That is why building secure optical communication systems has become a hot topic in many countries. A 3D trellis-coded modulation based on set-partitioning constellation mapping and four-winged fractional-order chaotic encryption was proposed to achieve highly reliable and secure optical transmission over short distances^[11]. Despite playing an important role in security enhancement^[10–13], chaotic encryption algorithms are vulnerable to breaches by quantum computers. In the realm of cryptography, post-quantum cryptography has emerged as a new standard designed to secure existing cryptographic algorithms against quantum computer attacks^[14–17]. This approach boasts exceptional quantum security, fast computing speed, reasonable communication overhead, and the ability to seamlessly replace conventional algorithms and protocols, making it highly versatile in application scenarios. The traditional information encryption method uses a key both parties know in communication. Therefore, if two individuals who have not been in contact before wish to communicate with each other, they do not possess the key required to decrypt the message. In such cases, the key must be exchanged through a communication channel. However, during this process, the key is vulnerable to interception by eavesdroppers, which renders the encryption ineffective. Asymmetric cryptography offers an encryption method that does not require both parties to agree on a common key and allows for key transmission without requiring a communication channel, reinforcing information transmission security. An asymmetric key consists of a public key for encryption and a private key for decryption. Although there is a relationship between the two keys, it is extremely challenging to calculate the private key from the public key. The McEliece encryption has outstanding advantages such as being code-based, having strong error correction abilities, high-security performance, and easy key management^[15–17].

Sign up for Chinese Optics Letters TOC. Get the latest issue of Chinese Optics Letters delivered right to you！Sign up now

In this paper, we propose a security-enhanced SDM transmission system based on multi-constellation shaping (MCS) to achieve better performance and higher security. First, the McEliece model is employed to encrypt information and resist quantum computer attacks to ensure the highest level of information security. To procure high-dimensional signal coding modulation, multiple users’ constellations are designed by utilizing MCS technology. Then 3D constellation data are sent into the system by 3D-CAP technology. Given that multi-user signals are inevitably subject to interference from noise during transmission across multiple channels, code-division multiplexing (CDM) technology allows us to achieve orthogonality among different user information. Finally, a seven-core weakly coupled optical transmission experimental platform is established to verify the effectiveness of our proposed scheme.

2. Principle of MCS and Asymmetric Encryption

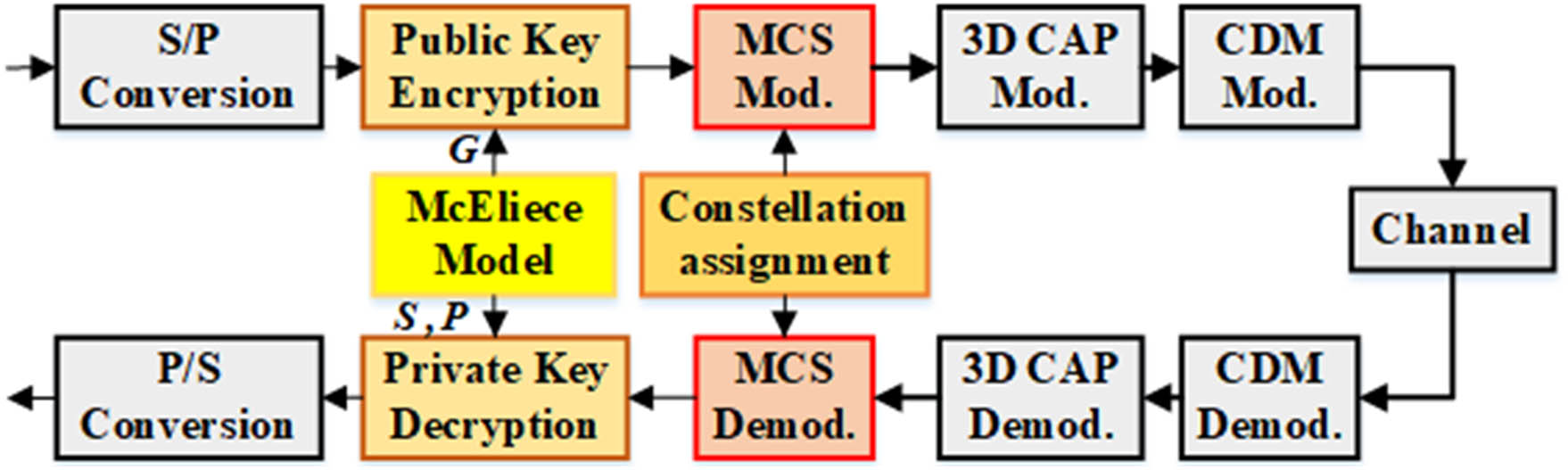
The schematic diagram of the MCS modulation based on asymmetric encryption is shown in Fig. 1, which can realize multi-user flexible coding and improve users’ information security. At the transmitter, we adopt the public key ( $G$ ) to encrypt information after serial-to-parallel (S/P) conversion. After encryption, the encrypted information is modulated into a 3D symbol string through the MCS modulator. As a result, different 3D-shaped constellations are combined to form a nonuniform constellation point distribution by probabilistic combination. Then, the 3D-CAP technology is applied to modulate the string further and obtain the users’ transmitted data. Finally, CDM technology is employed to orthogonalize different user information, which cannot only effectively reduce the correlation between user information, but also resist interchannel cross talk to a certain extent. Through SDM channel transmission, CDM demodulation is carried out to separate the multi-user information. Then 3D-CAP demodulation, MCS demodulation, private key decryption, and parallel-to-serial (P/S) conversion are performed on the separated data successively to obtain the binary data at the receiving end.

Figure 1.Schematic diagram of the proposed scheme.

We utilize the McEliece model based on the Goppa error-correcting code for generating public and private keys^[15–17]. Goppa error-correction codes belong to linear codes, and Goppa polynomials are $g (X) = \sum_{i = 0}^{t} g_{i} X^{i} \in F_{2^{m}} [X] .$ (1)

The finite field of order $q$ is represented by $GF (q)$ , and its $n$ -dimensional linear space can be represented by ${GF}^{n} (q)$ . The $[n, k, d]$ linear reducible Goppa code randomly generates a matrix $G$ of $k \times n$ order with $t$ error-correcting bits on $GF (q)$ , where the Goppa parameters are defined as $n = q^{m}$ , $d = 2 t + 1$ , $k = n - m t$ . A reversible nonsingular matrix $S$ of $k \times k$ order and an $n \times n$ order binary permutation matrix $P$ are randomly selected in a finite field $GF (q)$ . $H$ is the $(n - k) \times k$ order check matrix corresponding to $G$ ; then, we calculate $G^{'} = SGP$ that is disclosed as the public key, $H$ , $S$ , and $P$ as the private key.

When Alice sends a message to Bob, Bob’s public key $G^{'}$ is used to encrypt the plaintext $m$ , and the ciphertext $c$ is $c = m G^{'} + e,$ (2)where $e$ is the n-bit random error vector of weight $t$ in ${GF}^{n} (q)$ , $w (e) \leq t$ . When Bob receives ciphertext $c$ , he decrypts the ciphertext using the private key, $c^{'} = c P^{- 1} = m S G + e P^{- 1} .$ (3)

As $w (e P^{- 1}) = w (e)$ , Bob can acquire $c^{'} = m S$ according to the decoding algorithm of Goppa code, and then multiply with invertible matrix $S^{- 1}$ to get the message $m$ . In addition, McEliece’s security is based on error-correcting coding theory. Suppose there is a binary bit stream of 1024 length. If there are 50 error code words, then the error position has $C_{1024}^{50} \approx 3 \times 10^{85}$ , and it is very difficult to crack. However, one disadvantage of the McEliece model is that it requires a large public key matrix, which increases the redundancy of the system. The parameters of Goppa code adopted in this paper are $m = 4$ , $t = 2$ , and $q = 2$ , and the size of the obtained public key matrix is $8 \times 16$ .

Additionally, we provided a detailed explanation of the public–private key encryption process and its significance by taking examples. The user generates a set of asymmetric keys, keeps the private key, and broadcasts the public key. When Alice wants to communicate with Bob, Alice first sends a request to get Bob’s public key. After receiving the public key, Alice wants to send message $m$ to Bob, and then the information to be sent is encrypted with the public key $G^{'}$ and sent to Bob. After receiving the information, Bob uses its private key ( $S$ , $P$ , $H$ ) to decrypt it. If the link is eavesdropped, the listener cannot get the correct information except through the public key. In Fig. 2, although Bob1 gets the information of Bob2, without the private key of Bob2, the information cannot be cracked correctly.

Figure 2.Principle of asymmetric encryption.

The principle of MCS is to modulate multi-user data by adopting geometric shaping and probabilistic combination technology, so that the nonuniform distribution characteristics can be realized at the transmitter. Different geometric shaping schemes are employed for each user, so each user has a different constellation shape. Then, a nonuniform 3D probabilistic constellation is formed by probabilistic combination. To illustrate the MCS technique in detail, we take four users’ systems as examples. By employing the geometric shaping, four 3D subconstellations are designed for each user, as shown in Figs. 3(a)–3(d), and the combined constellation after probabilistic combination is shown in Fig. 3(e). Table 1 displays the mapping relationship between the binary symbols and the coordinates of each user’s constellation points. Hence, flexible coding modulation is realized by arranging the constellation points in a flexible manner. By calculating, users_1–4 have different constellations, with their average power being 2.43, 2.43, 2.11, and 2.95, respectively. Additionally, there is an exchange rule that governs the assignment of constellations to users, which is described as follows.

Step 1: If ber_x > 3.8 × 10⁻³

Con_0 = Con_x;

Con_x = Con_i; % i = 1:1:4

Con_i = Con_0;

end % Con_i represents ith constellation mapping

Step 2: If ber_xnew < 3.8 × 10⁻³

break out;

else

Con_0 = Con_x;

Con_x = Con_i+1;

Con_i+1 = Con_0;

end

Step 3: Repeat Step 2 until the bit error rate is less than 3.8 × 10⁻³

Table 1.

Mapping Relationship between Binary Symbols and Each Users’ Constellation Points Coordinates

Binary Data	Constellation Coordinates (p = 2.22, q = 1.41, u = 1.57, v = 2.42)
Binary Data	User_1	User_2	User_3	User_4
0000	(1, −1, −1)	(q, 0, q)	(q, 0, −1)	(0, v, 0)
0001	(1, 1, −1)	(q, 0, −q)	(0, q, −1)	(0, −v, 0)
0010	(−1, 1, −1)	(−q, 0, −q)	(−q, 0, −1)	(−p, p, 0)
0100	(−1, −1, −1)	(q, 0, q)	(0, −q, −1)	(−v, 0, 0)
1000	(1, −1, 1)	(0, q, q)	(q, 0, 1)	(p, 0, p)
1100	(1, 1, 1)	(0, q, −q)	(0, q, 1)	(p, 0, −p)
1010	(−1, 1, 1)	(0, −q, −q)	(−q, 0, 1)	(0, −p, −p)
1001	(−1, −1, 1)	(0, −q, q)	(0, −q, 1)	(−p, 0, p)
0110	(p, 0, p)	(q, q, 0)	(u, u, p)	(−p, p, 0)
0101	(p, 0, −p)	(q, −q, 0)	(u, u, −p)	(v, 0, 0)
0011	(−p, 0, p)	(−q, −q, 0)	(−u, −u, −p)	(p, p, 0)
1110	(−p, 0, p)	(−q, q, 0)	(−u, −u, p)	(0, p, p)
1011	(0, p, p)	(q, q, q)	(−u, u, p)	(0, −p, p)
1101	(0, p, −p)	(q, −q, −q)	(−u, u, −p)	(−p, 0, −p)
0111	(0, −p, −p)	(−q, −q, q)	(u, −u, −p)	(p, −p, 0)
1111	(0, −p, p)	(−q, q, −q)	(u, −u, p)	(0, p, −p)

Figure 3.Constellation diagram of (a) user_1, (b) user_2, (c) user_3, (d) user_4, and (e) multi-constellation combination. (f) Top view of (e).

By utilizing constellation exchange technology, we can achieve the desired performance adjustment in user bit error rate (BER).

3. Experiments and Results

The performance of the proposed scheme is verified by building a seven-core optical fiber transmission experimental platform, as displayed in Fig. 4. The specific modulation steps of offline digital signal processing (DSP) at the transmitter are also illustrated in Fig. 4. An arbitrary waveform generator (AWG, TekAWG70002A) with a sampling rate of 25 GSa/s is used for digital-to-analog conversion and amplification of electrical signals via an electric amplifier (EA). The Mach–Zehnder modulator (MZM) modulates the electrical signals over the optical carriers. An external cavity laser is employed to produce 193.4 THz, 1550 nm output light as the optical input of the MZM. The erbium-doped fiber amplifier (EDFA) is implemented to amplify the optical signals, enabling them to pass through multicore fiber channels with sufficient power. The seven-core fiber adopted is a commercial weakly coupled multicore fiber. The fan in device transmits the coupled data into seven-core optical fiber. At the receiver, a fan-out device sends the data of seven fiber cores into the single-core single-mode fiber. A variable optical attenuator (VOA) is used to adjust the received optical power. The optical signal in each fiber core is received and converted to an electrical signal using a photodiode (PD), which is collected by mixed signal oscilloscope (MSO, TekMSO73304DX) with a sampling rate of 50 GSa/s, and then sent to the offline DSP for demodulation. The specific demodulation steps of offline DSP at the receiver are reversed to that at the transmitter, which can perform the decryption to recover the original data. Finally, the raw binary data are compared to the received binary data by the BER counter.

Figure 4.Experimental setup.

Figure 5 exhibits that the BER curve varies with received optical power for back-to-back and core_1 reception. The BER decreases as the received optical power increases after transmission. Under the same received optical power, the BER is smaller after back-to-back transmission than after optical fiber transmission. These results are consistent with information theory, indicating that the scheme is feasible. When BER is $1 \times 10^{- 2}$ , the optical fiber transmission penalty is about 1.77 dB. Figure 5 also shows the constellation diagrams of all user information after back-to-back transmission and fiber transmission. The clear constellation diagram also indicates that the proposed scheme is feasible.

Figure 5.The BER varies with received optical power after back-to-back and multicore fiber transmission.

Figure 6 depicts the BERs of legitimate receivers and illegal receivers after transmission with seven cores as a function of received optical power. The BER of the legitimate receivers decreases with the increase of the received optical power, and the trend of the seven cores after the transmission is the same. For the same BER, the received optical power difference between the cores is about 1.00 dB at most. Moreover, the BER of illegal receivers is not sensitive to the received optical power and is always around 0.5. This means that the illegal receiver cannot receive accurate information after demodulation.

Figure 6.The BER varies with received optical power after seven-core fiber transmission.

Figure 7 displays the BER curves and constellation diagrams of different users at the receiver of core_2. The maximum difference in received optical power between different users is about 1.95 dB. Undoubtedly, user_3’s BER is the best under the same transmitting power due to its lowest constellation average power. Figure 7(a) also illustrates the received total constellation diagram, and Figs. 7(b)–7(e) are the received constellation diagram of each user when the received optical power is $- 14 dBm$ . The edge of the constellation diagram is visible, indicating that the user information can be received normally without error.

Figure 7.(a) BER curves versus received optical power, and (b)–(e) constellation graphs of users_1–4.

In addition, to prove the importance and security of private keys, we measure the BER under the wrong private key. Figure 8 shows the BER of the received data transmitted through core_3 with correct and different wrong private keys when the received optical power is $- 15 dBm$ . It is evident that whether all the three private keys $S$ , $P$ , and $H$ are wrong, or one of them is wrong, the BER is always around 0.5, and the received information cannot be acquired by correct demodulation.

Figure 8.BER curve of the wrong private key.

Furthermore, we showcase a delightful image featuring a lesser panda using the proposed McEliece model. Figure 9 shows the images with their corresponding histograms, both before and after encryption. Notably, the illegal receiver is confronted with nothing more than an indistinguishable blur, devoid of any relevant gray-scale information or even faulty histogram. However, the legal receiver enables one to get the correct image and histogram.

Figure 9.Images: (a) before encryption, (b) after illegal reception, (c) after legal reception. Histograms: (d) before encryption, (e) after illegal reception, (f) after legal reception.

4. Conclusions

To enhance the security of physical layer while improving system performance, we propose a high-security multicore optical transmission system based on MCS with asymmetric encryption. By incorporating MCS modulation and 3D-CAP modulation, we can achieve high-dimensional coding modulation, thereby enhancing the performance of the transmission system. The use of CDM enables orthogonal multi-user information and multiplexing transmission in both code slice and space dimensions. To verify the effectiveness of our proposed scheme, we conducted experiments on a 2-km, seven-core optical transmission platform. The results demonstrate the feasibility of our proposed scheme, as the received information can be accurately obtained using the correct private key. However, if one of private keys is missing or incorrect, the transmitted information will be completely miscoded and rendered unintelligible. Consequently, our proposed MCS scheme based on asymmetric encryption is a potential solution to improve the security of optical transmission networks in the future.

References

[1] D. L. Butler, M. J. Li, S. Li et al. Space division multiplexing in short reach optical interconnects. J. Lightwave Technol., 35, 677(2017).

[2] B. J. Puttnam, G. Rademacher, R. S. Luís. Space-division multiplexing for optical fiber communications. Optica, 8, 1186(2021).

[3] D. J. Richardson, J. M. Fini, L. E. Nelson. Space-division multiplexing in optical fibers. Nat. Photonics, 7, 354(2013).

[4] X. Li, M. Luo, Q. Yang. High-capacity optical transmission technologies in multi-core fiber. 16th International Conference on Optical Communications and Networks, 1(2017).

[5] H. Takara, T. Takahashi, K. Nakajima et al. Petabit/s optical transmission using multicore space-division-multiplexing. IEICE Trans. Commun., E97.B, 1259(2014).

[6] Z. Chen, S. G. Kang. Three-dimensional modulation formats with constant power for optical communications. Opt. Express, 19, 22358(2011).

[7] X. Sun, H. Zhang, Z. Zeng et al. A 3-D polarization quadrature amplitude modulation method and constellation mapping. China Commun., 12, 16(2015).

[8] J. Ren, B. Liu, X. Wu et al. Three-dimensional probabilistically shaped CAP modulation based on constellation design using regular tetrahedron cells. J. Lightw. Technol., 38, 1728(2020).

[9] C. Ni, B. Liu, J. Ren et al. Three-dimensional constellation diagram with a hierarchical level design for multi-core transmission. Opt. Express, 30, 2877(2022).

[10] Y. Zhang, N. Jiang, A. Zhao et al. Security enhancement in coherent OFDM optical transmission with chaotic three-dimensional constellation scrambling. J. Lightwave Technol., 40, 3749(2022).

[11] Y. Bai, B. Liu, X. Wu et al. Performance-enhanced three-dimensional Trellis coded modulation based on four-winged fractional-order chaotic encryption for physical layer security. J. Lightwave Technol., 40, 7701(2022).

[12] Y. Xiao, Y. Chen, C. Long et al. A novel hybrid secure method based on DNA encoding encryption and spiral scrambling in chaotic OFDM-PON. IEEE Photon. J., 12, 7201215(2020).

[13] F. Wang, B. Zhu, K. Wang et al. Physical layer encryption in DMT based on digital multi-scroll chaotic system. IEEE Photon. Technol. Lett., 32, 1303(2020).

[14] D. J. Bernstein, T. Lange. Post-quantum cryptography. Nature, 549, 188(2017).

[15] R. J. McEliece. A public-key cryptosystem based on algebraic coding theory(1978).

[16] J. C. Faugère, V. Gauthier-Umaña, A. Otmani et al. A distinguisher for high-rate McEliece cryptosystems. IEEE Trans. Inf. Theory, 59, 6830(2013).

[17] S. Yu, Q. Huang. Hard reliability-based ordered statistic decoding and its application to McEliece public key cryptosystem. IEEE Commun. Lett., 26, 490(2022).