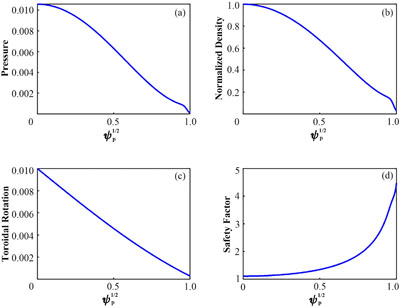
Fig. 1. Radial profiles of the key equilibrium quantities for HL-2A discharge 36 872 at 1 240 ms (a) The plasma pressure normalized by $B_{\mathrm{0}}^{\mathrm{2}}/{\mu }_{\mathrm{0}}$, (b) The normalized density, (c) The toroidal rotation frequency normalized by the on-axis Alfven frequency, (d) The safety factor

Fig. 2. The layout of the HL-2A plasma boundary and the position of the resonant magnetic perturbation coils (color online)

Fig. 3. The MARS-F computed $n=\mathrm{1}$ poloidal spectra of the vacuum field (a) and the total field perturbation (b), which includes the plasma response, compared the amplitude of the resonant harmonics for the perturbed radial field between the vacuum and the total response fields (c), plot shows the amplitude of normal displacement at the poloidal plane (d)

Fig. 4. The MARS-F computed amplitude of the resonant radial field perturbation $\left|b_{\mathrm{r}\mathrm{e}\mathrm{s}}^{\mathrm{1}}\right|$ near the plasma edge, for the vacuum field and the total field including the plasma response, as well as the plasma surface displacement near the X-point $\left|{\xi }_{\mathrm{n}}\right|$, while varying the coil phasing $\mathrm{\Delta }\varphi$ between the upper and lower rows (color online)

Fig. 5. Comparison of the poloidal spectra of the radial magnetic field perturbation computed with $n=\mathrm{1}$ for (a) the vacuum RMP field, (b) the total field including the resistive fluid plasma response, (c) the total field including the ideal fluid plasma response, and (d) the total field including the ideal-plasma kinetic response

Fig. 6. The computed poloidal distribution of the total response field (left panels) and the radial displacement of the plasma (right panels) caused by $n=\mathrm{1}$ RMP, assuming (a, b) the resistive fluid plasma model, (c, d) the ideal-plasma fluid model, and (e, f) ideal-plasma kinetic model

Fig. 7. MARS-F/K computed the total response field (external + plasma response) for three models at different rotation frequencies, including (a) the radial profiles of the m/n=4/1 resonant component and (b) the maximum amplitude of the poloidal Fourier harmonics (along the minor radius)

Fig. 8. The MARS-F computed growth rate of no-wall ideal external kink instability with $n=\mathrm{1}$ under various plasma pressure ${\beta }_N$

Fig. 9. The MARS-F/K computed plasma radial displacement amplitude near the X-point while varying ${\beta }_N$ in the fluid and full kinetic response model

Fig. 10. The MARS-K computed diagram of the relation between the plasma radial displacement amplitude near the X-point and ${\beta }_N$ in the different particles' ideal kinetic response model

Fig. 11. The real and imaginary parts of the normalized perturbed kinetic energy $\delta {\widehat{W}}_K$ associated with various drift kinetic effects of thermal ions and electrons, without (a) and with (b) inclusion of the particle collision effect

Fig. 12. Radial profiles illustrating various frequencies