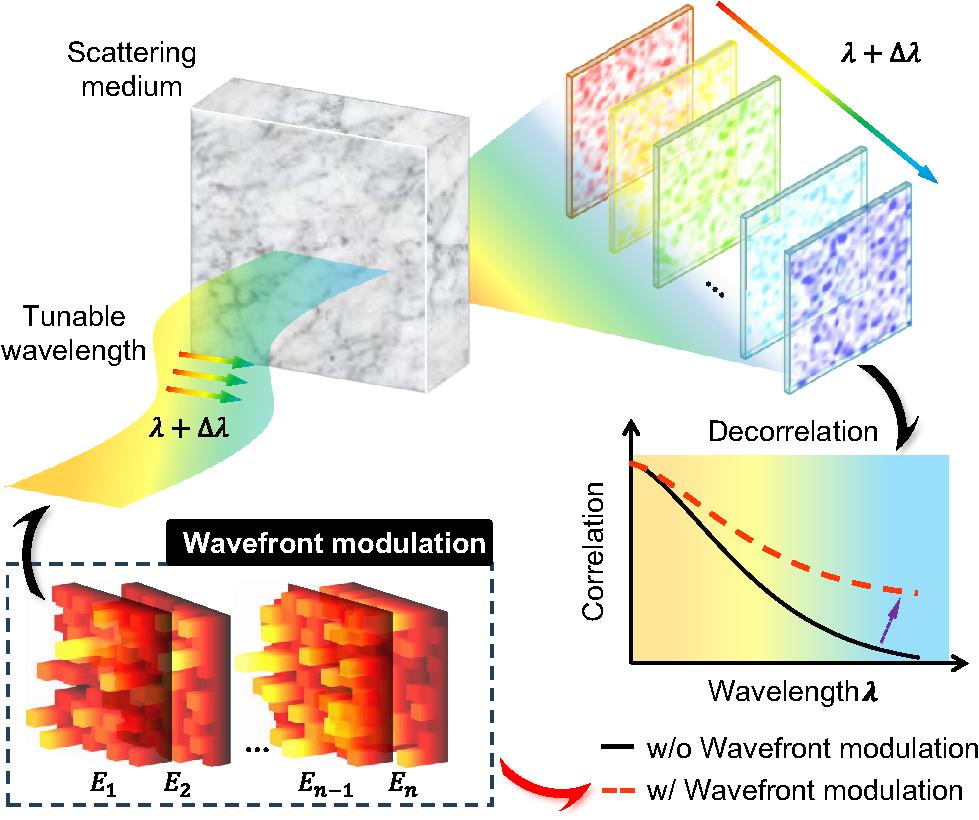
Fig. 1. Principal diagram of the spectral memory effect of a scattering medium. As detuning wavelengths increase, scattering characteristics evolve, leading to a decrease in the intensity correlation curve (solid black line, bottom right corner). Active wavefront modulation (bottom left corner) may significantly alter this decay (red dashed line, bottom right corner), indicating an enhanced spectral memory effect.

Fig. 2. FDTD simulation results of the spectral memory effect with excited scattering eigenchannels. The procedure begins with the characterization of a $25\times 25$ scattering matrix, which is then decomposed to identify scattering eigenchannels. (a) The correlation coefficients as functions of the detuning wavelength for three representative eigenchannels (high-, medium-, and low-transmission). (b) The correlation coefficients for 13 eigenchannels at three specific detuning wavelengths ($\mathrm{\Delta }\lambda =1$, 3, 5 nm). (c) The spectral detuning parameter $\sigma$, plotted as a linear function of the detuning wavelength. This plot compares numerical fitting results (in black) against theoretical predictions (in blue), highlighting their alignment. (d) The spectral memory effect’s range for 13 selected scattering eigenchannels, plotted against the transmission eigenvalue. Data points are represented by circles, whereas the fitting curve is shown with a dashed line. Error bars, calculated as standard deviations from five different scattering media that are macroscopically identical.

Fig. 3. Experimental setup of a nonholographic system with a tunable spectrum. This setup enables the nonholographic determination of the scattering matrix via phase-retrieval methods, facilitating the arrangement for the investigation of the relationship between the spectral memory effect and the coupling into eigenchannels. Tunable laser, ranges from 638 to 640 nm with a tuning step size of 0.1 nm; M, reflection mirror; HWP, half-wave plate; PBS, polarization beam splitter; BB, beam block; L1-L2, lenses ($f_1=7.5\mathrm{mm}$, $f_2=250\mathrm{mm}$); BS, beam splitter; SLM, spatial light modulator; MO1-MO2, microscopic objectives; scattering medium, a 1-mm-thick piece of resin with $\sim 100\text{-}\mu \mathrm{m}$-diameter alumina powder embedded (${\mu }_s=0.74{\mathrm{mm}}^{-1}$, ${\mu }_a=0.04{\mathrm{mm}}^{-1}$); P, polarizer; CCD, charge-coupled device. A termination computer is employed for programmable system control.

Fig. 4. Experimental results of the spectral memory effect with excited scattering eigenchannels. The scattering matrix for a piece of resin with embedded powder was characterized by a dimension of $400\times 400$. (a) The correlation coefficients as functions of the detuning wavelength for three representative eigenchannels (high-, medium-, and low-transmission). (b) The correlation coefficients for 41 eigenchannels, arranged in order of increasing eigenvalues, at three specific detuning wavelengths ($\mathrm{\Delta }\lambda =0.3$, 0.8, 1.3 nm). (c) The experimental data of the spectral detuning parameter $\sigma$, fitted and shown in red, displays a linear correlation with the detuning wavelength in black. (d) The spectral memory effect’s range for 13 selected scattering eigenchannels, plotted against the transmission eigenvalue. Data points are represented by circles, whereas the fitting curve is shown with a dashed line. Error bars, representing standard deviations, are derived from five independent experiments conducted at different translational positions of the sample.

Fig. 5. Simulation results of the spectral memory effect under practical conditions. The effects of absorption and finite bandwidth are individually explored. In the baseline scenario, the scattering medium has a thickness of $5\mu \mathrm{m}$ and a scattering coefficient ${\mu }_s=2.703{\mathrm{mm}}^{-1}$, illustrated with blue data and a fitting curve. To simulate absorption, an absorption effect ${\mu }_a=0.019{\mathrm{mm}}^{-1}$ is introduced, impacting the spectral memory effect. The impact of finite bandwidth is explored by employing a light source with a 2-nm bandwidth, centered at 639 nm. The outcomes are visualized with red and yellow data points and fitting curves, respectively.

Fig. 6. Schematic diagram of the FDTD simulation framework and results. (a) Visual representation of the FDTD simulation setup for the scattering medium. The structure incorporates numerous cylinders within a confined space, simulating the medium’s scattering properties. The boundaries are designed to perfectly absorb outgoing waves, ensuring an accurate depiction of wave propagation and scattering. (b) Absorption model correlation functions: displaying correlation coefficients as functions of scattering channel count for three detuning wavelengths (2, 4, and 6 nm). This graph provides evidence of how the spectral memory effect varies under the influence of material absorption within the scattering medium, showcasing different trends for each wavelength. (c) Finite bandwidth model correlation functions: exhibiting correlation coefficients across scattering channel counts for the same set of detuning wavelengths (2, 4, and 6 nm), under the finite bandwidth illumination scenario. This segment demonstrates the impact of bandwidth constraints on the spectral memory effect, highlighting how finite bandwidth can modulate the effect across different scattering channels.