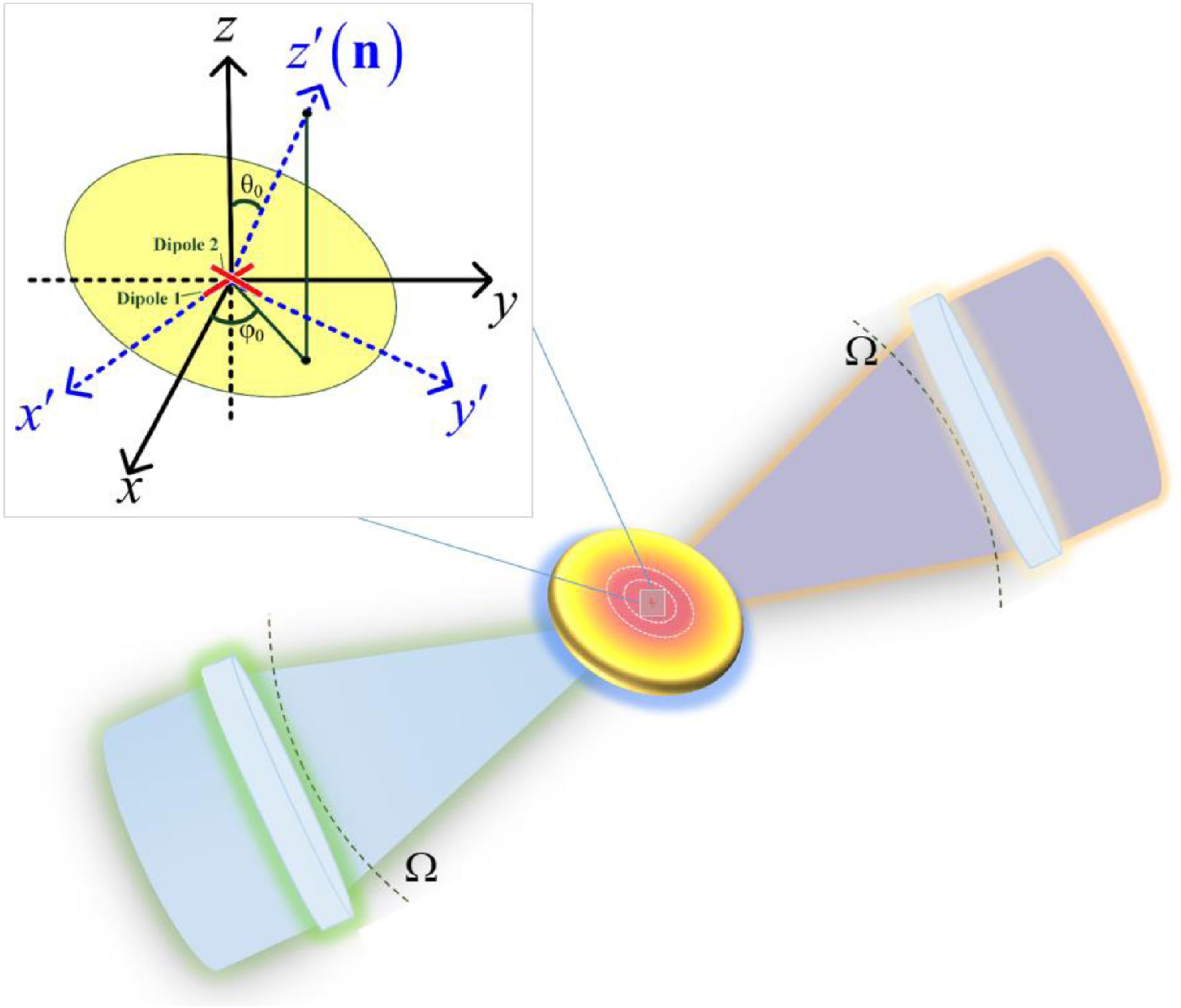
Yongxi Zeng, Yanzhong Yu, Jian Chen, Houan Teng, Musheng Chen, Pinghui Wu, Qiwen Zhan, "Spin angular momentum engineering within highly localized focal fields: from simple orientation to complex topologies," Photonics Res. 13, 995 (2025)
Search by keywords or author
- Photonics Research
- Vol. 13, Issue 4, 995 (2025)
Abstract
Set citation alerts for the article
Please enter your email address



