Yongxi Zeng, Yanzhong Yu, Jian Chen, Houan Teng, Musheng Chen, Pinghui Wu, Qiwen Zhan, "Spin angular momentum engineering within highly localized focal fields: from simple orientation to complex topologies," Photonics Res. 13, 995 (2025)
Search by keywords or author
- Photonics Research
- Vol. 13, Issue 4, 995 (2025)
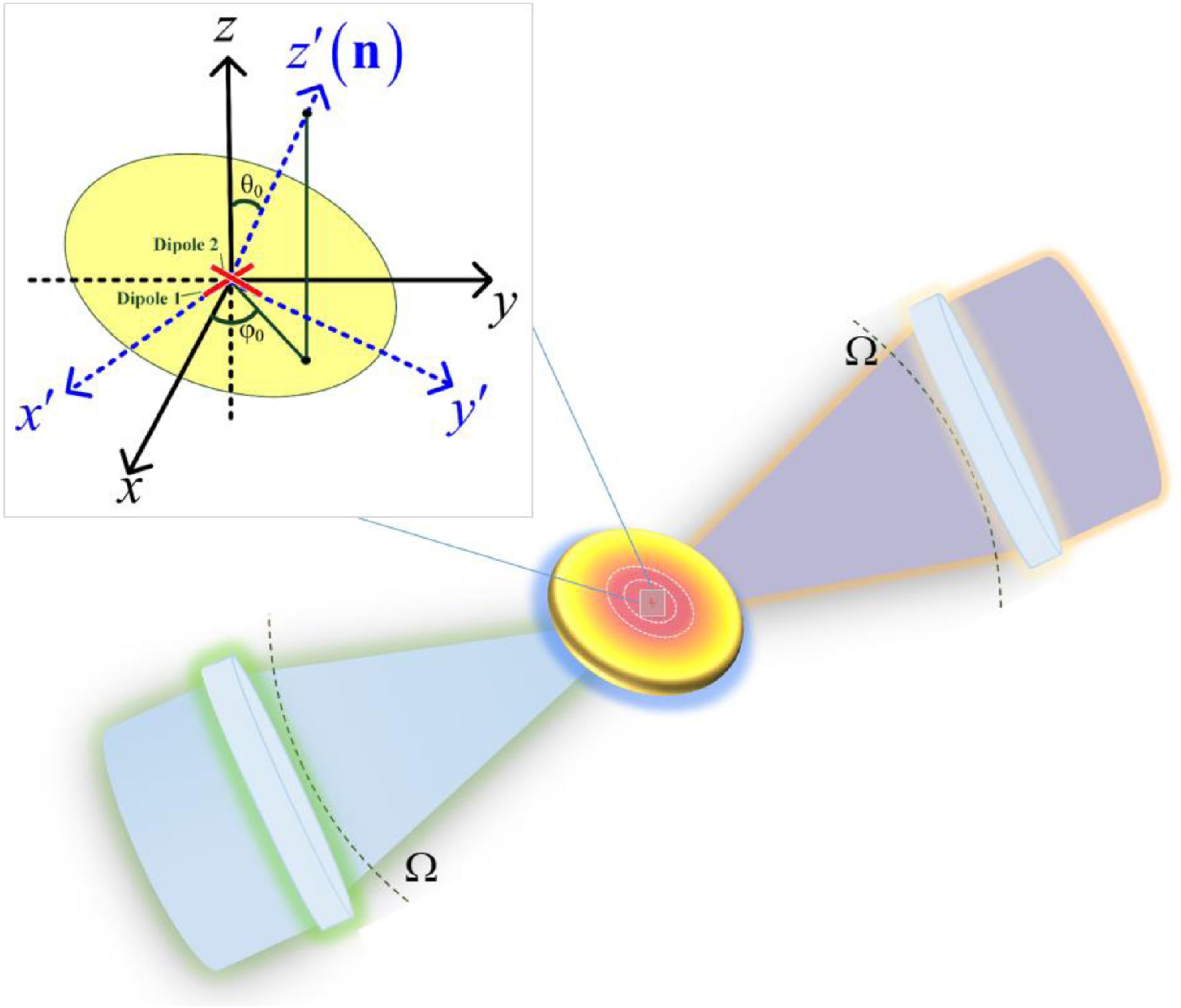
Fig. 1. Diagram of a 4 π

Fig. 2. Sub-diffraction-limited focal field with purely longitudinal SAM. (a) Intensity and polarization distribution of the required incident field. (b) Intensity and polarization distribution of the focus field in the three principal planes, and the opposite rotation directions of polarization are represented by white and black ellipses. (c) Line scanning of the focal field along the x y z S x S y S z
Fig. 3. Sub-diffraction-limited focal field with prescribed SAM, exemplified by ( θ 0 , φ 0 ) = ( 30 ° , 120 ° ) x y z S x S y S z x − y x − y
Fig. 4. Arrangement of MCAODP.
Fig. 5. Néel-type SAM skyrmion (a)–(f) and bimeron (g)–(l) with negative polarity in the x − y z x − y
Fig. 6. SAM skyrmions and bimerons in the y − z x − z y − z p = 1 v = 1 x − z p = 1 v = 1 y − z x − z p = 1 v = 1
Fig. 7. SAM skyrmions and bimerons in arbitrary prescribed planes. (a) is a Néel-type SAM skyrmion with p = − 1 v = 1 ( θ 0 , φ 0 ) = ( 40 ° , 60 ° ) p = − 1 v = 1 ( θ 0 , φ 0 ) = ( 45 ° , 45 ° ) p = 1 v = 1 ( θ 0 , φ 0 ) = ( 50 ° , 60 ° ) ( θ b , φ b ) = ( 90 ° , 0 ° ) p = − 1 v = 1 ( θ 0 , φ 0 ) = ( 45 ° , 45 ° ) ( θ b , φ b ) = ( 90 ° , 90 ° )
Fig. 8. Sub-diffraction-limited focal field with x x y z S x S y S z y − z y − z
Fig. 9. Sub-diffraction-limited focal field with purely transverse SAM, exemplified by ( θ 0 , φ 0 ) = ( 90 ° , 45 ° ) x y z S x S y S z x − y x − y
Fig. 10. Néel-type SAM skyrmion and bimeron with positive polarity in the x − y
Fig. 11. SAM anti-skyrmion and anti-bimeron with positive polarity in the x − y
Fig. 12. SAM bimeron with p = v = 1 φ r = 0 ° θ b = 90 ° φ b φ b
Fig. 13. Néel-type SAM bimeron with p = v = 1 φ r = 0 ° φ b = 45 ° θ b θ b
Fig. 14. SAM skyrmion and bimeron with p = − 1 v = 1 φ r φ r = 45 ° φ r = 90 °

Set citation alerts for the article
Please enter your email address



